Рассмотрим векторы 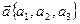 ,
, 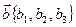 ,
, 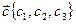 в ДПСК
в ДПСК 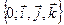 . Тогда, учитывая, что
. Тогда, учитывая, что
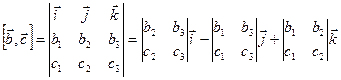 ,
,
получаем 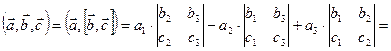
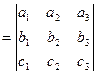 .
.
Пример. При каком 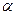 векторы
векторы 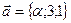 ,
, 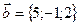 ,
, 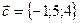 будут компланарны?
будут компланарны?
Решение:
Воспользуемся критерием компланарности. Векторы  ,
,  ,
,  компланарны тогда и только тогда, когда
компланарны тогда и только тогда, когда 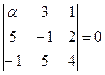 . Вычислим определитель и решим уравнение относительно
. Вычислим определитель и решим уравнение относительно 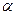 :
: 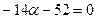 ;
; 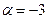 .
.
Пример. Даны векторы 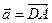 ,
, 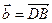 ,
, 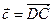 трёх рёбер тетраэдра
трёх рёбер тетраэдра 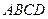 , выходящих из вершины
, выходящих из вершины 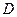 . Найти вектор
. Найти вектор 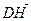 высоты тетраэдра, опущенной из вершины
высоты тетраэдра, опущенной из вершины 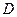 на плоскость
на плоскость 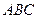 .
.
Решение:
Вектор 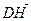 ортогонален плоскости
ортогонален плоскости 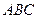 , т.е. коллинеарен вектору
, т.е. коллинеарен вектору 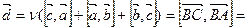


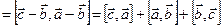 .
. 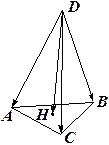 Следовательно, существует такое число
Следовательно, существует такое число 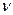 , что
, что 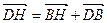 . Вектор
. Вектор 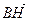 компланарен векторам
компланарен векторам 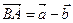 и
и 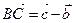 . Тогда найдутся такие числа
. Тогда найдутся такие числа 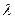 и
и 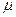 , что
, что 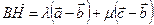 . Получаем для
. Получаем для 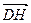 ,
, 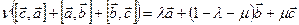 . Умножим обе части равенства скалярно на
. Умножим обе части равенства скалярно на 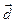 и получим:
и получим: 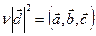 , т.е.
, т.е. 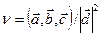 . Таким образом,
. Таким образом,
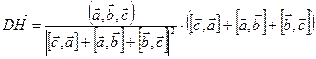 .
.
п. 11.2 Двойное векторное произведение
векторов
Определение 1. Двойным векторным произведением векторов  ,
,  ,
,  называют вектор
называют вектор 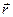 , равный векторному произведению одного из векторов тройки на векторное произведение оставшихся
, равный векторному произведению одного из векторов тройки на векторное произведение оставшихся 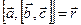 .
.
Замечание. Мнемоническое правило для запоминания: 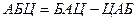 .
.
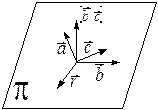 Теорема1.
Теорема1. 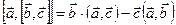 .
.
Доказательство:
| рис. 2.39 |
Из определения векторного произведения вектор 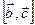 ортогонален плоскости
ортогонален плоскости 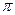 . Вектор
. Вектор 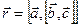 ортогонален плоскости, в которой лежат вектора
ортогонален плоскости, в которой лежат вектора  и
и 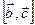 , т.е. лежит в плоскости
, т.е. лежит в плоскости 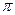 . Таким образом, вектор
. Таким образом, вектор 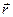 можно разложить по базису
можно разложить по базису 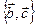 (в силу неколлинеарности векторов
(в силу неколлинеарности векторов  и
и  ):
): 
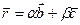 . Умножим последнее равенство скалярно на вектор
. Умножим последнее равенство скалярно на вектор  , получим
, получим 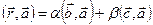 . Так как векторы
. Так как векторы 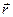 и
и  ортогональны, то
ортогональны, то 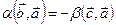 , т.е.
, т.е. 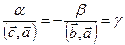 .
.
Итак, 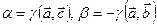 , учитывая коммутативность скалярного произведения. Покажем, что
, учитывая коммутативность скалярного произведения. Покажем, что 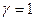 . Введём ДПСК
. Введём ДПСК 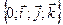 так, чтобы векторы
так, чтобы векторы 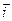 и
и  были коллинеарными. Тогда
были коллинеарными. Тогда 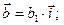
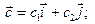
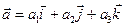 . Рассмотрим произведение
. Рассмотрим произведение 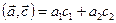 ,
, 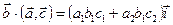 ;
; 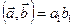 ,
, 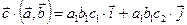 ;
;
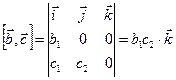 ,
, 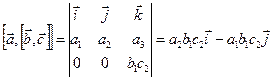 .
.
Сравнивая последнее равенство со следующим 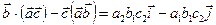 , получаем
, получаем 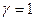 . ■
. ■
 2015-06-28
2015-06-28 637
637








