2015-06-28
402
Характеристика:
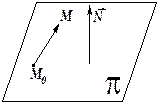Любая плоскость задаётся своей нормалью 
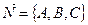(вектором, ортогональным данной плоскости) и точкой 
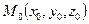, лежащей на этой плоскости.
Базовая задача:
Возьмём произвольную точку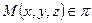 
. Вектор 
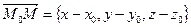лежит на плоскости 
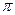. Так как 
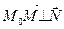, то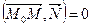 
. Тогда 
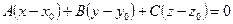. Раскрывая скобки, получим 
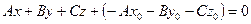. Обозначим 
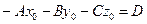. Тогда уравнение 
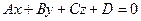называют общим уравнением плоскости.
Существуют и другие уравнения плоскости:
1. Уравнение плоскости в векторной форм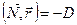е: 
, где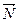 
– нормальный вектор данной плоскости, 
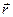– радиус-вектор точки 
. 
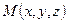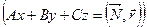
2. Нормальное уравнение плоскости. Так как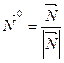 
, то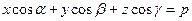 
, где: 
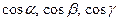– направляющие косинусы нормального вектора 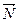, направленного из начала координат в сторону плоскости;
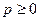– расстояние от начала координат до плоскости.
Нормальное уравнение плоскости получается путём умножения общего уравнения на нормирующий множитель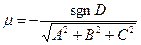 
, где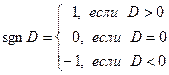 
, (signum - знак).
3. Уравнение плоскости в отрезках: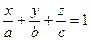 
, где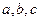 
– величины отрезков, которые отсекает плоскость на осях 
, 
, 
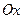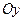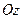соответственно.
