2015-06-28
239
Характеристики:
· нормальный вектор и точка;
· направляющий вектор и точка.
Базовые задачи:
1. Если на плоскости задана некоторая система координат, то прямую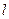 
можно провести через точку 
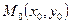перпендикулярно вектору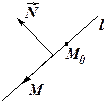 
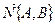, называемого
нормалью к данной прямой. Тогда, выбрав произвольную точку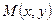 
так, чтобы векторы 
и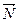 
были перпендикулярны, получим уравнение прямой :
, 
.
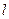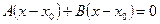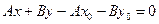Обозначим через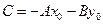 
. Тогда уравнение 
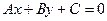называется общим уравнением прямой .
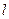2. Проведём прямую 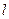через точку 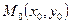параллельно вектору 
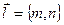, который называют направляющим вектором прямой 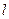. Выберем произвольную точку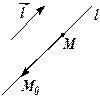 
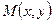так, чтобы векторы и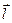 
были коллинеарными. Тогда 
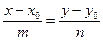– каноническое уравнение прямой.
Из последнего уравнения также можно получить общее уравнение прямой 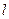, заметив, что векторы 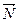и 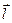перпендикулярны, причём 
, 
.
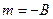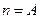Другие уравнения прямой:
1. Теперь проведём прямую 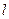через точк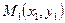и 
и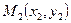 
. 
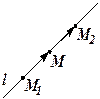Выберем произвольную точку 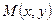так, чтобы векторы 
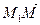и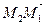 
были коллинеарными. Тогда уравнение 
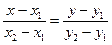задаёт прямую 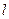, проходящую через точк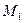и 
и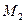 
.
2. Преобразуем последнее равенство:
|
|
|
; 
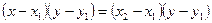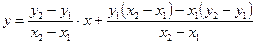. Тогда уравнение 
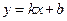также задаёт прямую 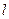, где:
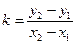- угловой коэффициент, причём 
(
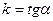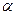- угол наклона прямо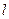й к оси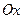 
);
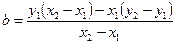- свободный коэффициент, равный длине отрезка, отсекаемого прямой от оси 
.
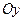Аналогично п. 12.1 можно получить нормальное уравнение прямой 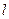и уравнение данной прямой в отрезках.
