1. Уравнение плоскости, проходящей через три различные точки, не лежащие на одной прямой.
Пусть точки 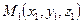 ,
, 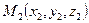 ,
, 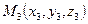 раз
раз 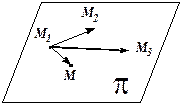 личные и не лежат на одной прямой. Выберем произвольную точку
личные и не лежат на одной прямой. Выберем произвольную точку 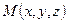 так, чтобы три вектора
так, чтобы три вектора 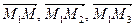 были компланарны. Используем критерий компланарности трёх векторов. Тогда уравнение
были компланарны. Используем критерий компланарности трёх векторов. Тогда уравнение 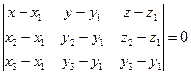 является уравнением искомой плоскости
является уравнением искомой плоскости 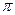 .
.
Угол между двумя плоскостями.
Определение 1. Пусть две плоскости 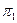 и
и 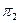 заданы общими уравнениями
заданы общими уравнениями 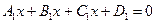 и
и 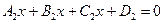 . Под углом между двумя плоскостями
. Под углом между двумя плоскостями 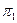 и
и 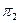 будем понимать угол между нормалями к этим плоскостям. Тогда:
будем понимать угол между нормалями к этим плоскостям. Тогда:
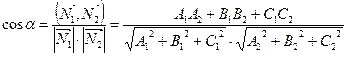 .
.
Условие перпендикулярности плоскостей 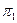 и
и 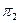 :
: 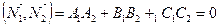 .
.
Условие параллельности плоскостей 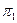 и
и 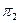 :
: 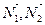 коллинеарные, т.е.
коллинеарные, т.е. 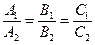 .
.
 2015-06-28
2015-06-28 382
382








