2015-06-28
1352
Глава 1. ЭЛЕМЕНТЫ ТЕОРИИ ВРЕМЕННЫХ РЯДОВ
В жизни вообще и экономике в частности нередко приходится иметь дело с результатами наблюдений некоторой величины, произведенных в различные моменты времени. Например, данные о количестве месячных осадков в некоторой местности (за несколько лет), данные о годовой урожайности пшеницы в стране, еженедельные цены на нефть, ежедневные курсы валют, акций компаний и т. д. Все это примеры временных рядов.
Определение 1.1. Последовательность наблюдений x (t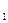 
), x (t 
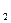),…, x (t 
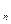) анализируемой величины (как правило, случайной) X, произведенных в различные моменты времени 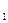t , t 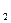,.., t 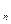, называется временным рядом. Мы будем рассматривать временные ряды с равноотстоящими моментами наблюдений, что позволит записывать их в следующей форме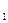: x 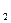, x ,…, x 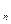. Сразу возникает вопрос: “ Чем отличается временной ряд от случайной выборки значений величины? “ Таких отличий два.
Во-первых, элементы случайной выборки являются статистически независимыми, а члены временного ряда – нет. Например, на сегодняшнюю величину биржевого индекса помимо других факторов влияют его значения за несколько предыдущих дней.
Во-вторых, члены временного ряда не являются, вообще говоря, одинаково распределенными: с течением времени могут изменяться характеристики случайной величины, например, среднее ожидаемое значение, и даже, что происходит значительно реже, закон распределения.
Поэтому не удается применить методы статистического анализа случайной выборки к анализу временных рядов. С другой стороны, взаимозависимость членов временного ряда определяет свою специфику построения прогнозных значений анализируемого показателя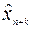 
по наблюденным значениям 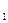x ,…, x .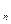
Значение элементов временного ряда формируется под воздействием ряда факторов. Обычно выделяют следующие 4 типа таких факторов и, следовательно, 4 компоненты, составляющие временные ряды.
А) Долговременные, формирующие общую (в длительной перспективе) тенденцию в изменении анализируемого признака x (t). К таким факторам можно отнести рост населения, изменения структуры потребления, экономическое развитие. Математически эта тенденция описывается с помощью той или иной неслучайной функции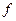 
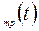, как правило, монотонной. Компонента временного ряда, описываемая такой функцией, называется трендом.
Б) Сезонные, формирующие периодически повторяющиеся в определенное время года колебания анализируемого признака.
Сезонная компонента описывается с помощью (неслучайной) периодической функции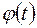 
.
В) Циклические (конъюнктурные) факторы, формирующие повторяемые изменения анализируемого признака в течение длительного периода. (волны экономической активности Кондратьева, демографические “ямы”, циклическая активность и т.п.). Циклическая компонента временного ряда, формируемая влиянием таких факторов, описывается с помощью неслучайной функции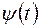 
, периодической с большим периодом.
Г) Случайные, не поддающиеся учету и регистрации. Воздействие таких факторов формирует случайную компоненту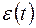 
и обуславливает стохастическую природу членов временного ряда.
Вовсе не обязательно, чтобы в формировании значений анализируемого временного ряда принимали участие все 4 фактора. Однако, всякий раз предполагается непременное участие случайных факторов.
Пример 1.1. В таблице 1 приведены данные о суммарных месячных расстояниях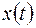 
(в тысячах милей), пройденных британскими авиалайнерами за 96 месяцев с января 1963г. по декабрь 1970г.
Таблица 1.
| Январь | ||||||||
| Февраль | ||||||||
| Март | ||||||||
| Апрель | ||||||||
| Май | ||||||||
| Июнь | ||||||||
| Июль | ||||||||
| Август | ||||||||
| Сентябрь | ||||||||
| Октябрь | ||||||||
| Ноябрь | ||||||||
| Декабрь |
На рисунке 1 приведен график данных:
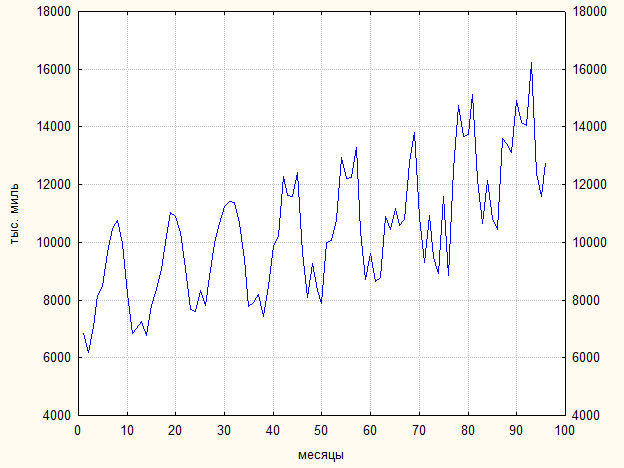рис.1
Элементарный анализ графика говорит о том, что данный временной ряд, помимо случайной компоненты, содержит временной тренд (растущий) и сезонную компоненту (с периодом 12 месяцев).
С помощью описанных выше компонент можно формировать различные модели временного ряда. Мы остановимся на аддитивной модели:
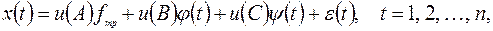(1.1)
где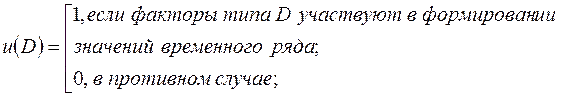 
.
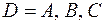Важнейшими задачами анализа временных рядов являются:
1. определение компонент, формирующих анализируемый временной ряд;
2. построения “хороших” оценок для тех неслучайных функций, которые присутствуют в разложении (1.1);
3. подбор модели, адекватно описывающей поведение случайной компоненты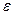 
(t); статистическое оценивание параметров этой модели.
Некоторые этапы и методы решения этих задач мы рассмотрим в следующих разделах.
Успешное решение задач 1-3 является основой для достижения главной прикладной цели исследования временного ряда: решения задач кратко- и среднесрочного прогноза значений временного ряда.
