Проверка соответствия распределения случайной компоненты нормальному закону распределения

Эту проверку можно осуществить, например, с помощью RS- критерия. Наблюдаемое значение статистики в этом критерии равно отношению размаха вариации случайной величины R= 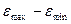к стандартному отклонению S= 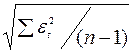. Наблюдаемое значение 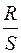сравнивается с критическими (табличными) верхней и нижней границами данного отношения. Если 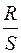попадает в интервал, заданный этими границами, то с заданным уровнем значимости принимается гипотеза о нормальном законе распределения случайной компоненты. В противном случае эта гипотеза отвергается. Например, при уровне значимости 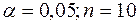нижняя граница равна 2,67, верхняя граница- 3,69.

3. Проверка равенства нулю математического ожидания случайной компоненты.

Проверка осуществляется с помощью t- критерия Стьюдента, с которым мы ранее уже встречались. Наблюдаемое значение определяется по формул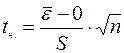е: , где 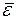- среднее арифметическое значение уровней остаточной компоненты 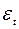; S - среднеквадратическое отклонение для этой последовательности.

Если 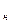|t |<t 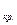, где t 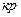- табличное значение статистики Стьюдента с заданным уровнем значимости 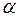и числом степени свободы n -1, то гипотеза о равенстве математического ожидания M(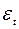)= нулю принимается.