Методы сглаживания временного ряда (выделение неслучайной компоненты)

Ранее уже отмечалось, что выявление основной тенденции изучаемого процесса, которая выражается неслучайной составляющей, является одной из важнейших задач исследования временного ряда. Методы выделения неслучайной компоненты можно условно поделить на два типа: аналитические и алгоритмические. Рассмотрим оба метода.

Аналитические методы выделения неслучайной составляющей временного ряда реализуются в рамках регрессионных моделей, в которых в роли результирующей переменной выступает переменная x (t), а в роли объясняющей переменной – время t, т.е. рассматривается модель:

.

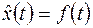Вначале выбирают вид функции f (t). Наиболее часто используются следующие функции:

f(t)=a₀+a₁t – линейная;

f(t)=a₀+a₁t+…+a_ntⁿ – полиномиальная;

f(t)= 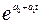- экспоненциальная;

f(t)= 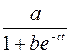- логистическая;

f(t)= 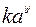- Гомперца.

Выбор вида моделирующей функции является ответственным этапом исследования, включающим в себя и визуальный (на основе графики временного ряда) анализ и содержательный анализ (с использованием аналитических методов).

Для примера рассмотрим метод последовательных разностей, применяемый для выбора вида полиномиальной функции. Этот метод используется в предположении, что, во-первых, отсутствуют сезонная и циклическая компоненты, во-вторых, тренд является достаточно гладким, чтобы его можно было аппроксимировать полиномом некоторой степени.

Пусть 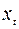, t= 1,2,…, n – исходный временной ряд. Рассмотрим ряд, состоящий из первых разностей: 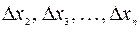, где 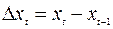. Если ряд x_t имеет линейный тренд x_t=a₀+a₁t+ε_t, то ряд Δ x_t, t= 2,…, n,не будет содержать тренда. Действительно,

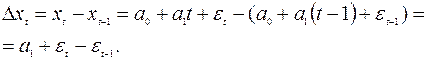
Аналогично можно показать, что если исходный ряд x_t имеет квадратичный тренд, то ряд, составленный из вторых разностей Δ² x₃, Δ² x ₄,…Δ² x _n, где Δ² x_t= Δ x_t -Δ x_{t- 1} =x_t -2x_{t- 1} +x_{t- 2}не содержит тренда. Если ряд содержит тренд, представляемый полиномом степени k, то ряд из разностей порядка k: 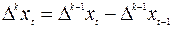должен содержать только случайную компоненту.

Предположим, что ε _t – некоррелированные случайные величины с математическим ожиданием M(ε _t)=0 и дисперсией D(ε _t)= σ ². Тогда математические ожидания для случайной составляющей разностей порядка k равно нулю: M(Δ ^kε _t)=0, а дисперсию можно оценить по формулам:

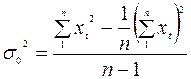- для исходного ряда;

(1.8)

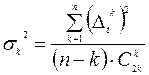, k =1,2,… - для разностного ряда k -го порядка,

где 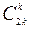– биномиальный коэффициент.

Порядок тренда не превышает числа k, начиная с которого оценки дисперсии 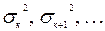становятся приблизительно постоянными.

Пример 1.4. В таблице 4 представлены данные о динамике цены акции нефтяной компании (руб.) по результатам торгов на бирже (временной интервал – шесть месяцев). Методом последовательных разностей определить порядок полинома, описывающего временной тренд.

Таблица 4.

цена,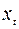

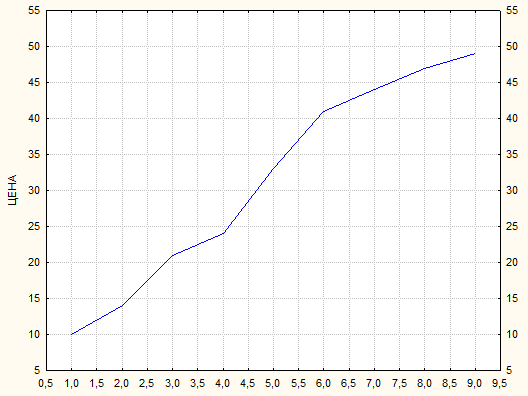
рис.3

Визуальный анализ свидетельствует о том, что временной ряд имеет явный тренд. Составим ряд из первых разностей:

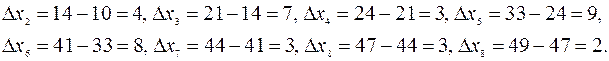
Дисперсия (см. (1.8))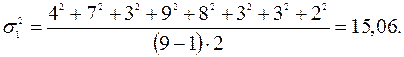

Ряд, составленный из вторых разностей, имеет вид: 3, -4, 6, -1, -5, 0, -1.

Дисперсия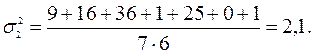

Разностный ряд порядка 3: -7, 10, -7, -4, 5, -1.

Дисперсия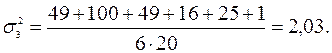

Мы видим, что дисперсия разностного ряда практически не изменилась. Таким образом, для аналитического выделения временного тренда достаточно использовать полином порядка не выше 2. Ниже мы убедимся, что уже полином первой степени дает хорошую оценку временному тренду.

После того, как вид модели определен, производится оценка параметров модели методом наименьших квадратов. Если выбрана линейная модель 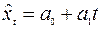, то система уравнений, с помощью которой производится оценивание, имеет вид:

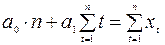
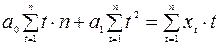
Замечания: 1. На практике обычно рассматривают несколько моделей и выбирают ту, для которой меньше сумма квадратов отклонений фактических данных от расчетных (RSS).

2. Для аппроксимации экономических процессов обычно используют полиномы не выше третьего порядка.

В основе алгоритмических методов выделения неслучайной составляющей временного ряда лежит простая идея: если разброс значений члена временного ряда x_t около своего среднего значения характеризуется дисперсией σ ² , то разброс среднего из N членов временного ряд а (x₁+ x₂+…+x_N)/N около того же значения будет характеризоваться дисперсией равной 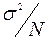. А уменьшение величины дисперсии как раз и означает сглаживание соответствующей траектории, элиминирование (частичное) случайной компоненты.

Рассмотрим самый простой метод алгоритмического сглаживания – метод (простого) скользящего среднего. В начале определяется интервал “усреднения” N – число членов ряда, по которым проводится усреднение. Как правило, N выбирается нечетным: 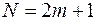. Затем, для первых N членов временного ряда вычисляется среднее арифметическое – это будет сглаженное значение ряда, находящееся в середине интервала сглаживания:

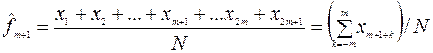. (1.9)

Далее интервал сглаживания сдвигается на один уровень вправо, повторяется вычисление среднего арифметического и т.д. Таким образом, сглаженное значение 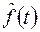временного ряда x(t) вычисляем по значениям 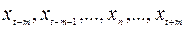по формуле

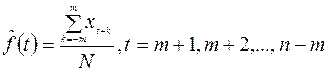. (1.10)

Поскольку, изменяя t от m+ 1 до n-m, мы как бы “скользим ” по оси времени, то и метод называется методом скользящего среднего (МСС).

Заметим, что в отличие от рассмотренных выше аналитических методов, МСС дает оценки 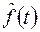значений временного тренда в момент времени t, хотя аналитическое задание тренда неизвестно.

Пример 1. 5. Методом скользящего среднего с шагом 3 провести сглаживание ряда из примера 4.

Рассчитаем средние значения членов ряда по «скользящему» интервалу длины 3:

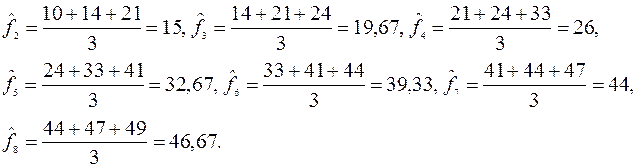
Исходный и «сглаженный» ряды представлены на графике:

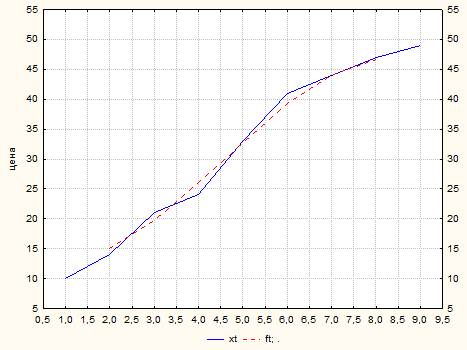
рис. 4

Метод простого скользящего среднего применим лишь для рядов, имеющих линейную тенденцию. В случае полиномиального тренда следует использовать формулу взвешенного среднего:

.

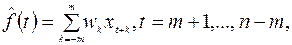
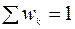Мы не будем подробно останавливаться на этой ситуации. К недостаткам МСС следует отнести то, что сглаживание происходит не во всех точных рядах: “теряются” моменты времени t =1,.., m,

n - m +1.