Стационарные временные ряды и их характеристики

Поиск модели, адекватно описывающей поведение случайной компоненты 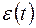анализируемого временного ряда 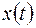, осуществляется, как правило, в рамках специального класса – класса стационарных временных рядов. Под стационарностью временного ряда понимают неизменность вероятностных свойств членов ряда во времени.

Определение 1.2: ряд 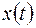называется строго стационарным (или стационарным в узком смысле), если совместное распределение вероятностей m наблюдений 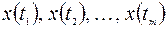такое же, как и для m наблюдений 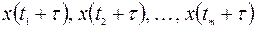, при любых 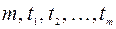и .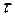

В частности, при m =1 из предположения о строгой стационарности временного ряда 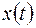следует, что закон распределения вероятности случайной величины 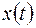не зависит от t, а значит, не зависят от t и все числовые характеристики.

Следовательно, математическое ожидание 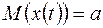, дисперсия D(x (t))=σ² случайной величины x (t), могут быть оценены по наблюдениям x ₁, x ₂, …, x_n:

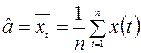- оценка математического ожидания (1.2)

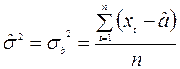- оценка дисперсии (1.3)

Простейшим примером стационарного вероятностного ряда является «белый шум», т.е. стационарный ряд у которого математическое ожидание равно нулю, а члены некоррелированы ().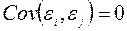

Из предположения о строгой стационарности временного ряда x (t) при 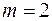следует, что степень тесноты связи между последовательностями наблюдений временных рядов x ₁, x ₂, …, x_n и x _{1+ τ} , x _{2+ τ} ,…, x_{n + τ} будет зависеть только от величины «сдвига по времени» (лага) τ и не будет зависеть от момента t. Как известно, степень тесноты статистической связи между двумя случайными величинами может быть измерена парным коэффициентом корреляции. Так как для стационарного временного ряда M (x (t))= M (x (t + τ))= a, D(x(t))=D(x(t+τ))= 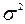, то этот коэффициент вычисляется по формуле

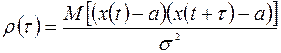. (1.4)

Коэффициент 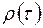измеряет корреляцию между членами одного и того же ряда. Поэтому его называют коэффициентом автокорреляции, а зависимость 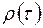от временного лага τ – автокорреляционной функцией.

Статистическое оценивание коэффициента 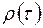осуществляют с помощью выборочного коэффициента автокорреляции, определяемого формулой

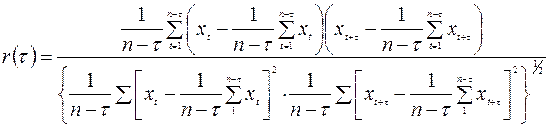. (1.5)

На практике более удобной для вычислений коэффициента 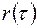является следующая формула:

.

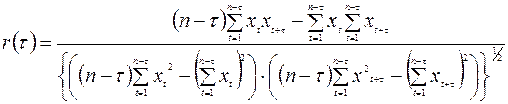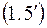
Для стационарного ряда в формуле (1.5) оценки среднего значения и дисперсии по n - τ наблюдениям заменяют оценками среднего и дисперсии всего ряда x ₁, x ₂,…, x_n. Тогда формула значительно упрощается:

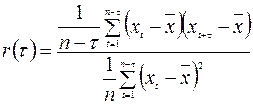, (1.6)

где .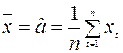

График значений r (τ) как функции от лага τ называется выборочной коррелограммой. Коррелограмма показывает насколько сильна линейная зависимость между членами ряда, разделенными (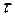 - 1) наблюдениями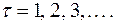

Для стационарного временного ряда, чем больше разнесены члены ряда по времени, тем слабее взаимосвязь этих членов и, соответственно, тем меньше (по модулю) значение 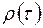. Более того, существует некоторое пороговое значение τ₀, начиная с которого все выборочные коэффициенты корреляции ρ (τ) будут равны нулю: ρ (τ)=0, 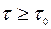_. В то же время, для выборочной автокорреляционной функции r (τ) свойство монотонного убывания (по абсолютной величине) часто нарушается, особенно при небольшом числе наблюдений.

Наряду с автокорреляционной функцией при исследовании стационарных временных рядов рассматривается частная автокорреляционная функция ρ _част(τ). При фиксированном значении временного лага τ частный коэффициент автокорреляции ρ _част(τ) измеряет корреляцию между членами временного ряда, разделенными τ тактами времени, при устранении влияния на эту взаимозависимость всех промежуточных членов временного ряда.

Например, частная автокорреляция 1-го порядка (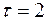) определяется следующим соотношением:

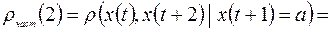
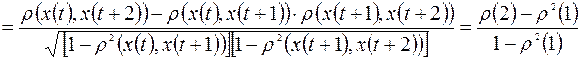
Аналогичным образом определяются выборочные частная автокорреляционная функция и частные коэффициенты автокорреляции. Например, выборочный частный коэффициент автокорреляции 1-го порядка между членами ряда x (t), x (t +2) при устранении влияния x (t +1) определяется по формуле:

r _част(2)= 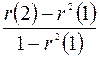. (1.7)

Пример 1.2. По данным таблицы 2 для временного ряда 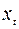найти среднее значение, дисперсию, коэффициенты автокорреляции (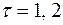) и частный коэффициент автокорреляции порядка 1.

Таблица 2.

год, t
спрос,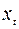

Среднее значение временного ряда находим по формуле (1.2):

.

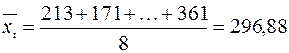Дисперсию вычисляем по формуле (1.3):

.

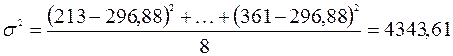Найдем коэффициент автокорреляции 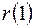, т.е. коэффициент корреляции между последовательностями семи пар наблюдени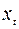й и :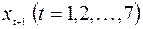

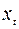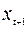Воспользуемся формулой 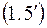. Вычисляем необходимые суммы:

;

;

;

;

.

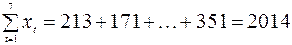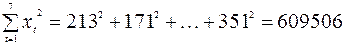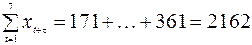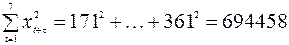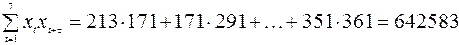Тогда коэффициент автокорреляции равен

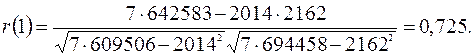
Аналогично вычисляя коэффициент автокорреляции 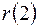по шести парам наблюдений, получаем: 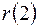=0,842.

Для определения частного коэффициента корреляции 1-го порядка 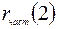между членами ряда 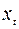и 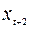при исключении влияния 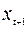применим формулу (1.7):

.

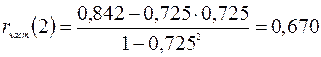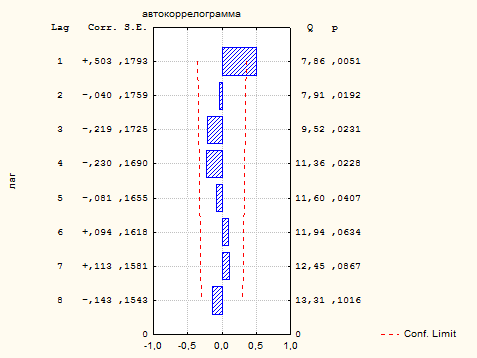
Пример 1.3. В таблице 3 приведены данные об уровне среднегодовых цен на рис, в амер. долларах за метрическую тонну. С помощью пакета прикладных программ «Статистика» рассчитана коррелограмма ряда для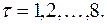

Таблица 3.

год	цена	год	цена	год	цена	год	цена

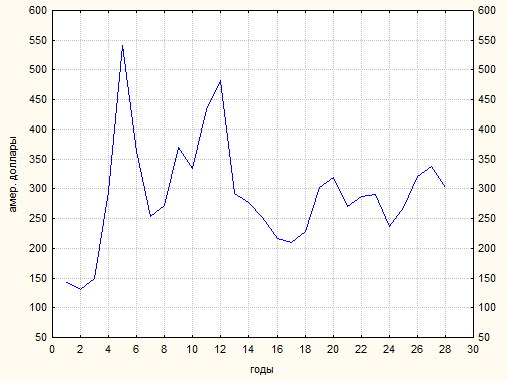
рис.2