ДРОБИ.
Основные определения:
1.  Обыкновенные дроби
Обыкновенные дроби
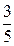
2.  Смешанные дроби.
Смешанные дроби.
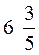
3.  Правило перевода смешанной дроби в неправильную:
Правило перевода смешанной дроби в неправильную:
4. Правило перевода неправильной дроби в смешанную дробь:
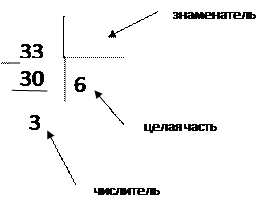
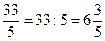
5. Правило нахождения общего знаменателя дробей (ОЗ):
1)найти НОК их знамкнателей;
2) определить для каждой дроби её дополнительный множитель;
3) умножить числитель и знаменатель каждой дроби на соответствующий дополнительный множител.
Перед приведением дробей к ОЗ их предварительно нужно сделать несократимыми.
| № п/п | Название действия | Что делаем? | Примеры. |
| Обыкновенные дроби | |||
| правильная дробь | числитель которой меньше знаменателя | 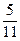
| |
| неправильная дробь | числитель которой больше знаменателя или равен ему | 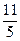
| |
| дробь как частное | черта дроби означает деление, то есть числитель можно разделить на знаменатель | 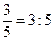
| |
| сравнение дробей с одинаковыми Ø знаменателями Ø числителями | Ø та дробь больше, у которой числитель больше, и та дробь меньше, у которой числитель меньше Ø та дробь больше, у которой знаменатель меньше, и наоборот, та дробь меньше, у которой знаменатель больше | 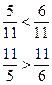
| |
| сравнение с 1 | Ø правильная дробь меньше 1 Ø неправильная дробь больше или равна 1 | 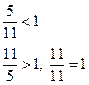
| |
| сложение (вычитание) дробей с одинаковыми знаменателями | складываем или вычитаем числители, а знаменатель оставляем прежним | 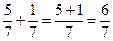
| |
| сравнение дробей с разными знаменателями и числителями | 1) приводим дроби к общему знаменателю(см правило нахождения ОЗ) 2) сравниваем как дроби с одинаковыми знаменателями (см п.4) | 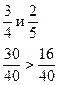
| |
| сложение и вычитание дробей с разными знаменателями | 1) приводим дроби к общему знаменателю (см правило нахождения общего знаменателя) 2) складываем или вычитаем как дроби с одинаковыми знаменателями (см правило №3) | 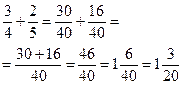
| |
| умножение дроби на натуральное число | 1 способ умножаем числитель дроби на это натуральное число 2 способ делим знаменатель на это натуральное число (если он делится без остатка) | 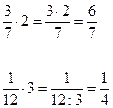
| |
| умножение дроби на дробь | умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби также умножаем на знаменатель второй дроби | 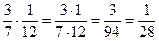
| |
| деление дроби на натуральное число | 1 способ делим на это число числитель дроби (если он делится без остатка) 2 способ умножаем знаменатель на это число | 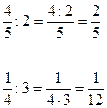
| |
| деление дроби на дробь | 1)первую дробь переписываем 2) знак деления заменяем на умножение 3)у второй дроби числитель меняем со знаменателем («переворачиваем вверх ногами») 3) выполняем умножение по правилу №6 | 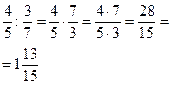
| |
| основное свойство дроби | числитель и знаменатель дроби можно умножать или делить на одно и тоже число | 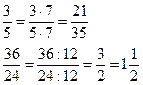
| |
| сокращение дробей | деление числителя и знаменателя на одно и то же число, большее единицы | 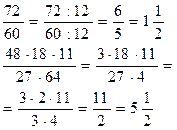
| |
| Ø нахождение дроби числа Ø нахождение числа по его дроби | Ø нужно это число разделить на знаменатель дроби и результат умножить на его числитель Ø нужно данную величину разделить на числитель дроби и результат умножить на её знаменатель | 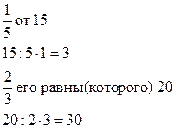
| |
| Смешанные дроби | |||
| сложение (вычитание) | складываем (вычитаем) целые части с целыми, а дробными с дробными | 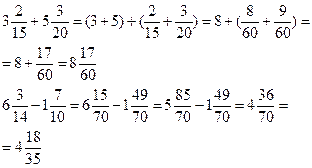
| |
| умножение (деление) | 1) переводим в неправильную дробь 2) умножаем или делим как обыкновенные дроби (см п. 10,12) | 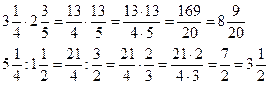
| |
| сравнение | из двух больше то, целая часть которого больше, если целые части чисел равны, то больше то, число, дробная часть которого больше | 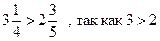
|
Соглашение о порядке выполнения действий, принятое для выражений.
1.Если выражение без скобок содержит действия одной ступени, то действия выполняются в порядке их записи слева направо.
2. Если выражение без скобок содержит действия разных ступеней, то сначала выполняются действия третьей ступени – возведение в степень, затем второй – умножение и деление и, наконец, первой – сложение и вычитание.
3. Если выражение содержит скобки, то сначала выполняются действия в скобках, а затем остальные, причем порядок их выполнения определяется пунктами 1 и 2.
 2015-06-28
2015-06-28 530
530







