Осью называется направленная прямая.
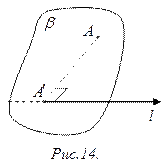
Определение 1. Проекцией точки 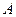 на ось
на ось 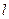 называется основание
называется основание 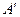 перпендикуляра
перпендикуляра 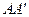 , опущенного из точки
, опущенного из точки 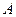 на ось
на ось 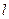 (рис.14).
(рис.14).
Чтобы в пространстве найти проекцию точки 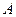 на ось
на ось 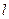 , нужно через точку
, нужно через точку 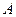 провести плоскость
провести плоскость 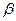 перпендикулярную оси
перпендикулярную оси 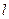 . Точка
. Точка 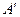 , пересечения плоскости
, пересечения плоскости 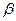 и оси
и оси 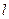 , будет искомой проекцией.
, будет искомой проекцией.
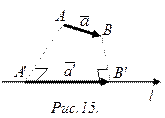
Определение 2. Компонентой вектора 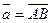 относительно оси
относительно оси 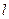 называется вектор
называется вектор 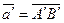 (рис.15), где
(рис.15), где 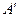 ‑ проекция на ось
‑ проекция на ось 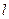 начала
начала 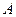 вектора
вектора  , а
, а 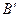 ‑ проекция на ось
‑ проекция на ось 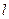 конца
конца 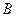 вектора
вектора  .
.
Определение 3. Проекцией вектора  на ось
на ось 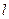 называется скаляр
называется скаляр 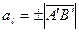 , равный длине компоненты
, равный длине компоненты 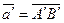 относительно оси
относительно оси 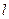 , взятой со знаком «+», если направление компоненты совпадает с направлением оси
, взятой со знаком «+», если направление компоненты совпадает с направлением оси 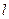 , и со знаком «‑», если направление компоненты противоположно направлению оси
, и со знаком «‑», если направление компоненты противоположно направлению оси 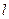 . Проекция вектора
. Проекция вектора  на ось
на ось 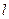 обозначается
обозначается 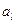 или
или 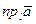 .
.
Теорема. Проекция вектора  на ось
на ось 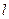 равна произведению длины
равна произведению длины 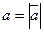 вектора на косинус угла между направлением вектора и направлением оси, т.е.
вектора на косинус угла между направлением вектора и направлением оси, т.е.
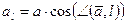 .
.
Доказательство. Пусть 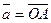 и
и 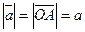 .
.
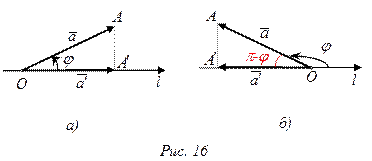
1. Если угол 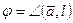 ‑ острый, то направление компоненты
‑ острый, то направление компоненты 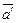 совпадает с направление оси
совпадает с направление оси 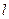 (рис.16 а). Тогда
(рис.16 а). Тогда 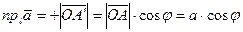 .
.
2. Если угол 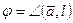 ‑ тупой, то направление компоненты
‑ тупой, то направление компоненты 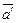 противоположно направлению оси
противоположно направлению оси 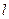 (рис.16 б). Тогда
(рис.16 б). Тогда
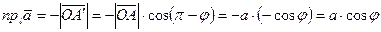 . □
. □
Свойства проекции.
1. 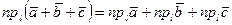 .
.
2. 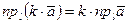 .
.
 2015-06-28
2015-06-28 869
869








