Доминирование стратегий

Лабораторная работа № 4. Матричные игры без седловых точек

Оптимальные стратегии игроков в играх без седловых точек могут быть найдены путем решения пары двойственных задач линейной оптимизации

Определение стратегий игрока I	Определение стратегий игрока II

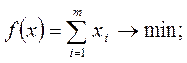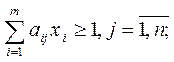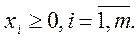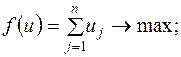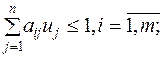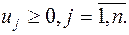Цена игры и вероятности применения стратегий игроками I и II равны:

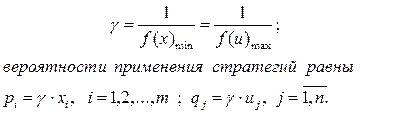
Доминирование стратегий.

Говорят, что некоторая стратегия 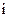первого игрока (задаваемая i -й строкой платежной матрицы) доминируется некоторой другой его стратегией k, если все элементы строки 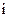не больше соответствующих элементов строки k, т.е.

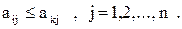
В свою очередь, некоторая стратегия 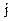второго игрока (задаваемая 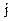-м столбцом платежной матрицы) доминируется его некоторой другой стратегией 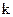, если все элементы столбца 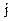не меньше соответствующих элементов столбца :

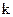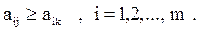
Наличие доминирования позволяет сократить размеры исходной платежной матрицы путем исключения доминируемых (заведомо невыгодных) стратегий игроков.

Пример. Рассмотрим платежную матрицу

.

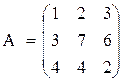Здесь первая стратегия игрока I доминируется его второй стратегией (все элементы первой строки меньше соответствующих элементов второй). Для игрока II стратегия 2 доминируется его первой стратегией (все элементы второго столбца больше либо равны соответствующим элементам первого).

После исключения доминируемых стратегий получим новую матрицу игры меньшего размера

,

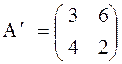в которой доминируемые стратегии отсутствуют.