Одним из недостатков рассмотренных методов является высокая степень интерполяционного многочлена, что не всегда является желательным. Разбиение же исходного отрезка на частичные и построение на них отдельных интерполяционных многочленов приводит к тому, что в точках стыка многочленов производные разрывны. Этого недостатка лишены интерполирующие функции, построенные на основе сплайнов.
| Сплайном на отрезке [a, b]называется функция, непрерывная на отрезке вместе со своими производными до заданного порядка включительно, которая на частичных промежутках этого отрезка описывается различными алгебраическими многочленами. |
Рассмотрим методику построения сплайна, основанного на алгебраических многочленах третьей степени, т.е. так называемую, кубическую сплайн – интерполяцию.
Как и ранее, считаем заданной таблицу значений функции 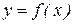 в точках a=x0 , x1, x2 ,…, xn = b. На каждом из отрезков [ xi-1, x i ] многочлен Pi(x) будем искать в виде
в точках a=x0 , x1, x2 ,…, xn = b. На каждом из отрезков [ xi-1, x i ] многочлен Pi(x) будем искать в виде
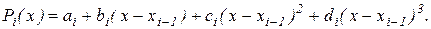
Таким образом, общее число многочленов равно n, а число неизвестных коэффициентов,- 4n. Поэтому для их определения необходимо такое же количество условий.
Потребуем, чтобы каждый многочлен в крайних точках своего отрезка удовлетворял условиям
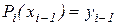 ,
, 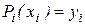 ,
, 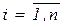 ,
,
что даёт 2n соотношений. Далее, потребуем, чтобы во внутренних узловых точках первая и вторая производные интерполирующей функции были непрерывными, т.е.
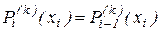 ,
, 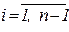 ,
, 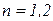 .
.
Это даёт ещё 2(n-1) ограничений. Для получения двух недостающих можно дополнительно потребовать, что в крайних точках отрезка интерполирующая функция имела нулевую кривизну, т.е.,
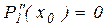 ,
, 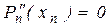
Таким образом, для определения коэффициентов многочленов имеем систему уравнений.
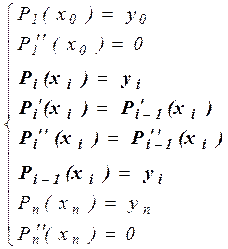
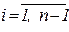 ,
,
которая оказывается линейной. В том случае, когда узловые точки являются равноотстоящими, т.е. 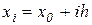 , она существенно упрощается и принимает вид
, она существенно упрощается и принимает вид
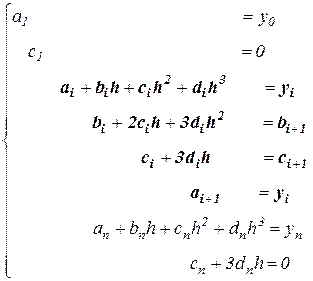
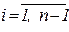 .
.
В частности, для трёх равноотстоящих узлов, т.е. n=2, имеем
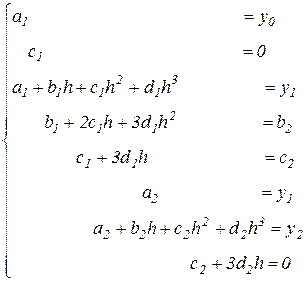
которая легко решается в общем виде. Действительно, из 1-го, 2-го, 5-го и 6-го уравнений следует 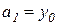 ,
, 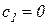 ,
, 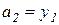 и
и 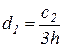 , а оставшаяся часть после традиционных преобразований приводится к треугольному виду
, а оставшаяся часть после традиционных преобразований приводится к треугольному виду
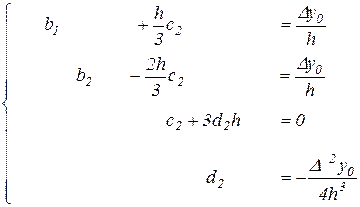 .
.
Варианты индивидуальных заданий
На промежутке [ a, b ] составить таблицу значений функции y=f(x) в (n+1)-ой равностоящих узловых точках. По этой таблице построить интерполяционные многочлены Лагранжа и Ньютона. В обоих случаях определить приближённые значения функции в точке 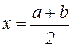 по формуле
по формуле 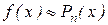 . Оценить погрешность
. Оценить погрешность 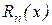 полученных значений, сравнить её с “точной ” погрешностью
полученных значений, сравнить её с “точной ” погрешностью 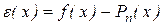 .
.
В вариантах 1-12 считать 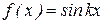 ,
, 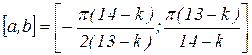 ,
,
в вариантах 13-25, - 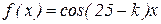 ,
, 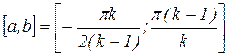 ,
,
где 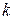 - номер варианта. Значение
- номер варианта. Значение 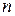 задается преподавателем.
задается преподавателем.
 2015-06-24
2015-06-24 495
495








