Рассмотрим формулу Ньютона (2.7) и предположим, что узлы являются равноотстоящими, а именно, 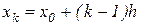 , где
, где 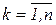 . Сделаем в ней замену
. Сделаем в ней замену 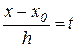 и учтя (2.11), получим
и учтя (2.11), получим
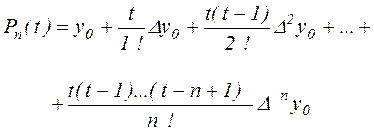 (2.13) (2.13) |
Это и есть многочлен Ньютона для равноотстоящих узлов, а погрешность интерполяции при его использовании оценивается выражением (2.12).
Отметим, что с увеличением порядка значение конечной разности 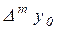 убывает. Поэтому нередко требуемая точность вычисления значения функции достигается при меньшем количестве слагаемых, т.е. при меньшем числе использованных узловых точек. В связи с этим, в зависимости от расположения значения x среди массива значений x0 , x1, … xn на основе (2.7) формируют частные формулы, используемые для интерполяции в начале, конце и середине таблицы. Рассмотрим эти случаи.
убывает. Поэтому нередко требуемая точность вычисления значения функции достигается при меньшем количестве слагаемых, т.е. при меньшем числе использованных узловых точек. В связи с этим, в зависимости от расположения значения x среди массива значений x0 , x1, … xn на основе (2.7) формируют частные формулы, используемые для интерполяции в начале, конце и середине таблицы. Рассмотрим эти случаи.
Пусть значение x близко к x0 . Тогда выбирая для интерполяции узловые точки x0 , x0 + h, x0 +m h получим
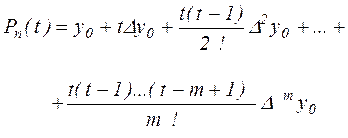 (2.14), (2.14), |
её погрешность, в соответствии с (2.12)
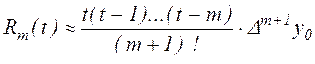 |
Пусть теперь значение x близко к xn, т.е. к концу таблицы. Тогда выбирая для интерполяции узлы xn, xn – h,…, xn –mh и сделав замену 

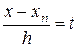 из (2.7) получаем
из (2.7) получаем
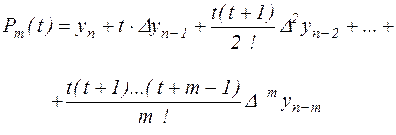 (2.15), (2.15), |
погрешность интерполяции
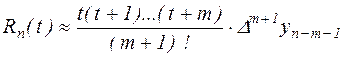 . . |
Если значение x близко к некоторому xk, расположенному в средней части таблицы, то для интерполяции обычно используют точки xk, xk + h, xk –h, …, xk+mh, xk-mh Соответствующий интерполяционный многочлен также получается из (2.7) и после замены 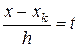 принимаем
принимаем
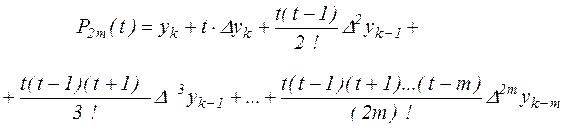 (2.16), (2.16), |
его погрешность оценивается выражением.
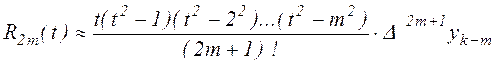 . . |
Интерполяционному многочлену (2.16) можно придать более симметричный вид. Так, разбивая нечётные слагаемые, начиная с третьего, на два, и группируя с чётными, получим
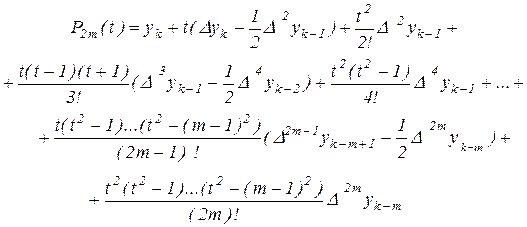
Представим теперь разности в скобках в виде
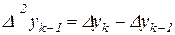 ,
, 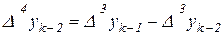 и т.д., получим многочлен,
и т.д., получим многочлен,
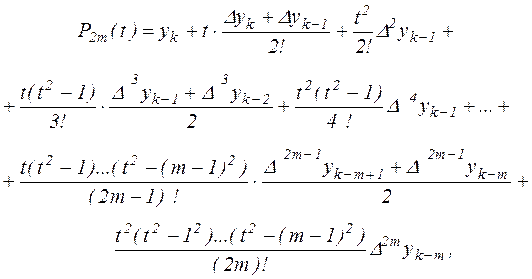 |
который называется интерполяционным многочленом Ньютона – Стирлинга.
 2015-06-24
2015-06-24 859
859








