Обычно процесс решения уравнения
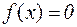 , (4.1)
, (4.1)
где 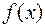 - некоторая непрерывная функция, распадается на два этапа.
- некоторая непрерывная функция, распадается на два этапа.
Первый из них заключается в установлении промежутка [ a, b ], на котором находится, по крайней мере, один корень уравнения (4.1). Этот этап называется отделением корней и может осуществляться различными способами. Один из них базируется на фундаментальном свойстве непрерывных функций, описанном теоремой Больцано-Коши:
Пусть функция 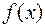 непрерывна на отрезке [ a, b ] и на его концах принимает значения разных знаков. Тогда существует внутренняя точка непрерывна на отрезке [ a, b ] и на его концах принимает значения разных знаков. Тогда существует внутренняя точка 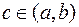 , в которой , в которой 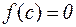 . .
|
Геометрически это означает, что при выполнении указанных условий график функции 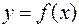 на отрезке [ a, b ], хотя бы один раз, пересечёт ось ox (Рисунок 4.1).
на отрезке [ a, b ], хотя бы один раз, пересечёт ось ox (Рисунок 4.1).


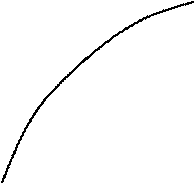




Рисунок 4.1. Иллюстрация к теореме Больцано-Коши
Отсюда следует, что для отделения корней уравнения (4.1) на первоначально заданном отрезке [ А; В ] необходимо с некоторым шагом h провести вычисление функции в точках 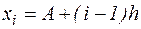 и выделить тот или те отрезки
и выделить тот или те отрезки 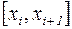 , для которых
, для которых 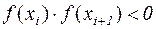 . Если с выбранным значением h такой промежуток выбрать не удалось, то необходимо повторить вычисления, уменьшая до разумных пределов значение h.
. Если с выбранным значением h такой промежуток выбрать не удалось, то необходимо повторить вычисления, уменьшая до разумных пределов значение h.
Другой способ отделения корней, - графический. При современном уровне развития вычислительной техники он, по-видимому, является и более предпочтительным. Заключается в построении графика функции 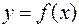 на промежутке [ A; B ] и в установлении, исходя из графика, отрезка [ a, b ], на котором он пересекает ось ох.
на промежутке [ A; B ] и в установлении, исходя из графика, отрезка [ a, b ], на котором он пересекает ось ох.
Замечание. На теореме Больцано-Коши основан один из методов решения нелинейных уравнений, - метод половинного деления. Он состоит в следующем. Пусть установлен отрезок [ a, b ], на котором 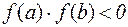 . Далее, рассматривается середина этого отрезка точка
. Далее, рассматривается середина этого отрезка точка 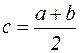 , определяется
, определяется 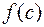 и из отрезков [ a; c ], [ c; b ] выбирается тот, на котором функция
и из отрезков [ a; c ], [ c; b ] выбирается тот, на котором функция 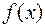 меняет знак.
меняет знак.
На выбранном отрезке, обозначим его через [ a1, b1 ], величина которого равна 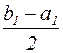 , снова рассматривается середина отрезка
, снова рассматривается середина отрезка 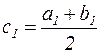 , определяется
, определяется 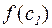 и из отрезков [ a1; c1 ], [ c1; b1 ] выбирается тот, на котором
и из отрезков [ a1; c1 ], [ c1; b1 ] выбирается тот, на котором 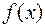 изменяет знак. Он обозначается через [ a2, b2 ] и процедура повторяется. На n - ом шаге величина отрезка [ an, bn ] равна
изменяет знак. Он обозначается через [ a2, b2 ] и процедура повторяется. На n - ом шаге величина отрезка [ an, bn ] равна 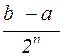 . Если она меньше
. Если она меньше 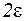 , где
, где 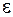 - требуемая точность решения уравнения, то процесс последовательного деления завершается и в качестве приближенного решения выбирается
- требуемая точность решения уравнения, то процесс последовательного деления завершается и в качестве приближенного решения выбирается 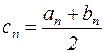 .
.
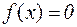 , (4.1)
, (4.1)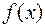 - некоторая непрерывная функция, распадается на два этапа.
- некоторая непрерывная функция, распадается на два этапа.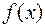 непрерывна на отрезке [ a, b ] и на его концах принимает значения разных знаков. Тогда существует внутренняя точка
непрерывна на отрезке [ a, b ] и на его концах принимает значения разных знаков. Тогда существует внутренняя точка 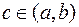 , в которой
, в которой 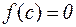 .
.
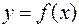 на отрезке [ a, b ], хотя бы один раз, пересечёт ось ox (Рисунок 4.1).
на отрезке [ a, b ], хотя бы один раз, пересечёт ось ox (Рисунок 4.1).







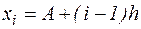 и выделить тот или те отрезки
и выделить тот или те отрезки 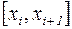 , для которых
, для которых 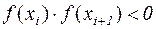 . Если с выбранным значением h такой промежуток выбрать не удалось, то необходимо повторить вычисления, уменьшая до разумных пределов значение h.
. Если с выбранным значением h такой промежуток выбрать не удалось, то необходимо повторить вычисления, уменьшая до разумных пределов значение h.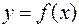 на промежутке [ A; B ] и в установлении, исходя из графика, отрезка [ a, b ], на котором он пересекает ось ох.
на промежутке [ A; B ] и в установлении, исходя из графика, отрезка [ a, b ], на котором он пересекает ось ох.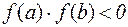 . Далее, рассматривается середина этого отрезка точка
. Далее, рассматривается середина этого отрезка точка 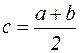 , определяется
, определяется 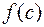 и из отрезков [ a; c ], [ c; b ] выбирается тот, на котором функция
и из отрезков [ a; c ], [ c; b ] выбирается тот, на котором функция 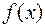 меняет знак.
меняет знак.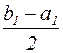 , снова рассматривается середина отрезка
, снова рассматривается середина отрезка 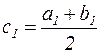 , определяется
, определяется 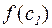 и из отрезков [ a1; c1 ], [ c1; b1 ] выбирается тот, на котором
и из отрезков [ a1; c1 ], [ c1; b1 ] выбирается тот, на котором 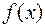 изменяет знак. Он обозначается через [ a2, b2 ] и процедура повторяется. На n - ом шаге величина отрезка [ an, bn ] равна
изменяет знак. Он обозначается через [ a2, b2 ] и процедура повторяется. На n - ом шаге величина отрезка [ an, bn ] равна 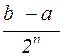 . Если она меньше
. Если она меньше 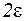 , где
, где 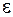 - требуемая точность решения уравнения, то процесс последовательного деления завершается и в качестве приближенного решения выбирается
- требуемая точность решения уравнения, то процесс последовательного деления завершается и в качестве приближенного решения выбирается 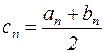 .
. 2015-06-24
2015-06-24 315
315








