Для описания сходимости вычислительного процесса и оценки  погрешности приближённого решения необходимы дополнительные понятия.
погрешности приближённого решения необходимы дополнительные понятия.
Понятие нормы. Нормой вектора х, обозначается 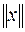 , называется величина удовлетворяющая условиям:
, называется величина удовлетворяющая условиям:
1. 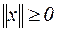 ;
;
2. 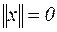

 х=0; (3.6)
х=0; (3.6)
3. 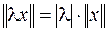 ;
;
4. 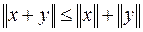 .
.
В теории метрических пространств получили распространение следующие типы норм:
1. 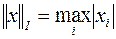 ;
;
2. 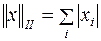 ;
;
3. 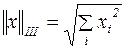 .
.
В зависимости от типа геометрической фигуры, получаемой в трёхмерном пространстве, описываемой условием 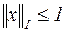 , первая из них называется кубической, вторая,- октаэдрической и третья,- сферической.
, первая из них называется кубической, вторая,- октаэдрической и третья,- сферической.
Нормой матрицы А, обозначается 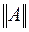 , называется величина, удовлетворяющая помимо требований (3.6) дополнительному условию
, называется величина, удовлетворяющая помимо требований (3.6) дополнительному условию
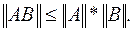
Обычно, используются одна из следующих норм:
1. 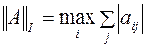 ;
;
2. 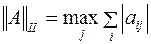 ;
;
3. 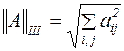 .
.
При одновременном использовании норм необходимо их согласование. А именно, норма вектора первого типа используется с нормой матрицы первого типа и т.д.
Понятие расстояния. Расстоянием между векторами x, y, обозначается символом 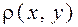 , называется величина
, называется величина
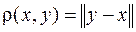 .
.
Из свойства 4 (3.6) следует важное для дальнейшего, так называемое, неравенство треугольника
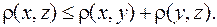
Действительно,
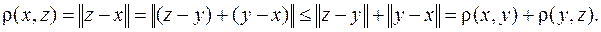
Сжимающие отображения. Пусть F,- некоторое отображение в линейном пространстве векторов. Оно называется сжимающим,- если существует такое число 
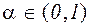 , что для любых векторов x, y выполняется соотношение
, что для любых векторов x, y выполняется соотношение
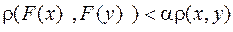 .
.
Применительно к нормальной форме системы уравнений (3.3) в качестве F рассмотрим правую часть системы уравнений. А именно,
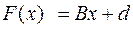 .
.
Тогда
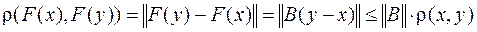 .
.
Таким образом, для того, чтобы отображение, определяемое системой (3.3) было сжимающим достаточно, чтобы одна из норм матрицы В была меньше 1.
Понятие сходимости. Пусть 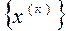 , где к = 1, 2, …,- некоторая бесконечная последовательность векторов. Говорят, что она сходится к вектору х по норме, если
, где к = 1, 2, …,- некоторая бесконечная последовательность векторов. Говорят, что она сходится к вектору х по норме, если
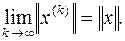
Последовательность 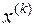 сходится к вектору
сходится к вектору 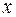 покомпонентно, если
покомпонентно, если
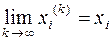 для
для 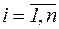 .
.
Нетрудно показать, что два эти понятия в некотором роде эквивалентны. А именно, если последовательность 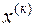 сходится по норме, то она сходится покомпонентно и наоборот.
сходится по норме, то она сходится покомпонентно и наоборот.
При анализе сходимости последовательностей центральное место принадлежит признаку Коши:
Последовательность 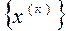 сходится тогда и только тогда, когда для сходится тогда и только тогда, когда для 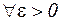 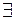 такой номер такой номер 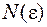 , что для , что для 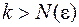 и и 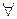 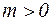 выполняется выполняется 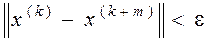 (или (или 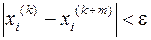 для для 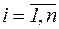 ). ). |
Сходимость итерационного процесса. Оценка погрешности. Пусть 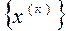 ,- итерационная последовательность, т.е.
,- итерационная последовательность, т.е.
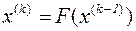 , (3.7)
, (3.7)
где 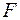 ,- сжимающее отображение с коэффициентом сжатия
,- сжимающее отображение с коэффициентом сжатия 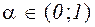 .
.
Рассмотрим 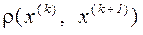 . По индукции имеем
. По индукции имеем
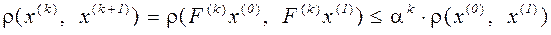 . (3.8)
. (3.8)
Далее, по свойству треугольников и с учетом (3.8), справедливым оказывается соотношение
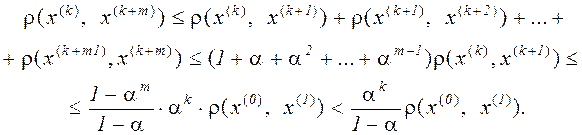 (3.9)
(3.9)
Потребовав теперь, чтобы
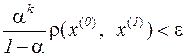 ,
,
очевидно, можно найти номер 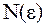 , начиная с которого
, начиная с которого 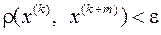 для
для 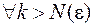 , m > 0.
, m > 0.
Таким образом, для сжимающего отображения признак Коши выполнен и, следовательно, итерационный процесс (3.7) сходится.
Оценим теперь погрешность к -го приближения, а именно, величину 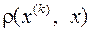 , где х - точное решение. С этой целью рассмотрим соотношение (см. (3.9))
, где х - точное решение. С этой целью рассмотрим соотношение (см. (3.9))
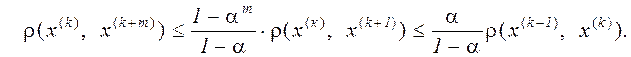
Переходя в нём к пределу при 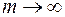 , получим, таким образом,
, получим, таким образом,
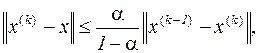 (3.10)
(3.10)
и доказанным становится утверждение:
| Если одна из норм матрицы B системы уравнений (3.3) меньше единицы, то итерационный процесс (3.4) является сходящимся при любом начальном приближении. Погрешность к -го приближения описывается соотношением (3.10). |
3.5 Приведение системы Ax=b к нормальному виду
Из предыдущего следует, что успех приближённого решения системы линейных алгебраических уравнений (3.1) во многом определяется возможностью её приведения к нормальному виду (3.3), для которого выполняется достаточные условия сходимости. Приведём некоторые соображения и рекомендации на этот счёт.
Первый вариант. Рассмотрим систему
Ах=b.
Представим матрицу А в виде суммы А=А1+А2, где det А1 ≠ 0. Тогда
(А1+А2) x=b,
отсюда
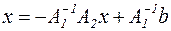 .
.
Обозначив через 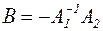 ,
, 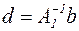 , получим
, получим
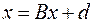 ,
,
что и требовалось. Тогда для того, чтобы обеспечить выполнение достаточного условия сходимости 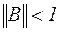 , в качестве А1 достаточно взять матрицу близкую к А, т.е. А1≈А, в качестве А2, - «малую» матрицу
, в качестве А1 достаточно взять матрицу близкую к А, т.е. А1≈А, в качестве А2, - «малую» матрицу 
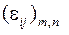 .
.
Поясним это предложение на примере. Рассмотрим
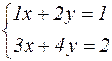 ,
,
Здесь 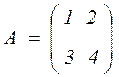 . Пусть
. Пусть
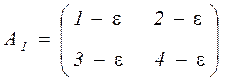 ,
,
Тогда 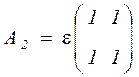 . Найдём
. Найдём 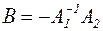 .
.
Имеем det А1 = -2 ≠ 0 и
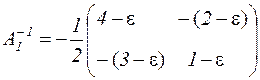 .
.
Тогда
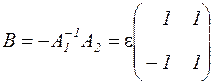
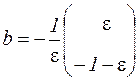
и система принимает вид
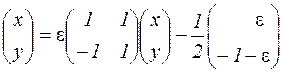 .
.
Очевидно, для сходимости метода итераций достаточно взять 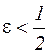 .
.
Второй вариант. Состоит в следующем. Путём эквивалентных преобразований стараются добиться того, чтобы диагональные элементы в матрице А доминировали в левой части соответствующих уравнений, т.е. были по модулю существенно больше остальных. После этого каждое из уравнений делят на 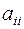 и, первое уравнение разрешают относительно
и, первое уравнение разрешают относительно 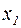 второе,- относительно
второе,- относительно 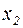 и т.д.
и т.д.
В качестве примера рассмотрим следующую систему
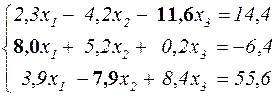
В результате анализа коэффициентов левой части уравнений производится их перестановка
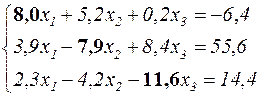
и для обеспечения доминирования во втором уравнении коэффициента 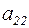 , который пока равен -7,9, ко второму уравнению прибавляется третье. В результате этого имеем
, который пока равен -7,9, ко второму уравнению прибавляется третье. В результате этого имеем
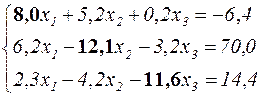
или, в нормальной форме,
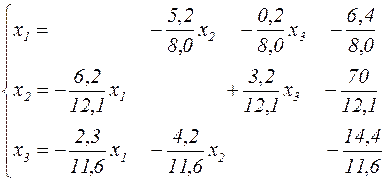 .
.
Здесь матрица
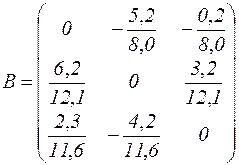 ,
,
очевидно, её норма 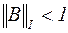 , и, следовательно, формируемый ею итерационный процесс сходится.
, и, следовательно, формируемый ею итерационный процесс сходится.
Третий вариант. Является обоснованным теоретически, формализуемым и, по этой причине, пожалуй, наиболее удобным. Он заключается в следующем.
Рассмотрим систему (3.11)
Ax=b
и предположим, что det А1 ≠ 0. Умножим обе части на 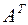 , получим
, получим
A1 x=b1,
где A1=АТА, b1= AT b. Здесь матрица A1 является симметрической, т.е. 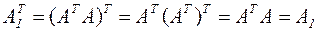 , причём её диагональные элементы
, причём её диагональные элементы 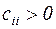 , в противном случае, по крайней мере, один из столбцов матрицы А равен нулю и, следовательно, det А = 0. Далее деля уравнение на диагональные элементы
, в противном случае, по крайней мере, один из столбцов матрицы А равен нулю и, следовательно, det А = 0. Далее деля уравнение на диагональные элементы 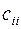 и, разрешая их относительно
и, разрешая их относительно 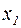 ,
, 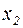 и т.д. получим нормальную систему
и т.д. получим нормальную систему
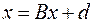 ,
,
где 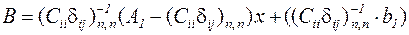 .
.
Показано, что для нормальной системы, полученной таким образом, метод Зейделя сходится.
Варианты индивидуальных заданий
1. При помощи ручного просчета найти решение системы линейных уравнений Аx=b методом Жордана – Гаусса, заданную своей расширенной матрицей согласно варианта задания. Вычисления провести с выбором определяющего элемента.
2. Написать программу решения системы методом Зейделя Аx=b, заданной своей расширенной матрицей. Максимальное количество уравнений в системе равно восьми. Исходные данные программы - расширенная матрица системы и значение допустимой погрешности. Выходные данные - вектор-столбец Х решения системы, проверка решения А*x и количество итераций, выполненное для получении решения.
Варианты систем для задания 1
| № 1 -6 -2 -4 68 -4 2 5 -1 -3 -1 -5 43 | № 2 -5 3 2 -24 3 3 5 -29 -4 -1 5 -43 | № 3 -1 1 1 5 1 2 -5 -6 -2 -5 2 -25 | № 4 -2 4 -3 -2 -4 -1 2 5 -5 1 1 4 | № 5 -1 -2 -2 7 1 -3 -4 -3 3 -3 -2 -25 |
| № 6 -6 -1 5 6 -6 -2 -6 32 -6 -3 5 14 | № 7 -4 -4 -4 40 3 4 4 -37 2 -1 -6 26 | № 8 1 -3 -5 2 2 1 4 -17 4 -6 1 -19 | № 9 -4 -2 -5 16 1 -6 5 7 -4 3 1 -28 | № 10 -4 -3 4 -21 3 1 5 12 5 5 2 30 |
| № 11 -3 1 -1 -6 -4 -2 3 15 -2 1 -5 -18 | № 12 5 -6 5 20 -1 -4 -1 14 1 2 3 -28 | № 13 2 5 -1 -41 -2 5 1 -29 2 -4 -3 14 | № 14 1 -6 4 65 2 2 5 28 -1 -3 2 25 | № 15 5 5 -4 -42 -2 4 -1 -9 -2 4 -5 -21 |
| № 16 1 5 -3 -5 -5 5 -4 30 -4 -5 4 15 | № 17 4 1 -5 11 3 4 2 1 1 5 5 -10 | № 18 -5 2 -2 25 -5 -2 -3 30 -6 5 -6 14 | № 19 -1 -4 -1 22 -5 -4 -2 46 -6 -1 -1 40 | № 20 5 -6 -2 15 -6 2 -6 30 -5 -4 -4 57 |
| № 21 -6 2 -5 37 4 -6 -4 16 4 4 2 -42 | № 22 -3 5 1 17 1 1 -3 5 1 -4 5 -12 | № 23 4 -5 -2 -3 -4 5 -1 3 -2 -5 1 39 | № 24 -5 1 -3 -7 3 -1 -5 -35 1 4 1 -13 | № 25 -1 -4 -6 -17 -4 2 1 -10 5 5 -4 63 |
 2015-06-24
2015-06-24 1354
1354








