В этом случае уравнение (4.1) приводится к виду
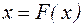 (4.5)
(4.5)
Далее, выбирается начальное приближение 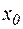 к решению и на основе (4.5) по правилу
к решению и на основе (4.5) по правилу
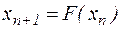 (4.6)
(4.6)
строится последовательность 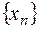 .
.
Рассмотрим отображение, формируемое функцией 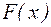 . Пусть
. Пусть 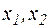 , - некоторые произвольные значения переменной
, - некоторые произвольные значения переменной 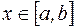 , оценим величину
, оценим величину 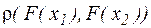 . Имеем
. Имеем
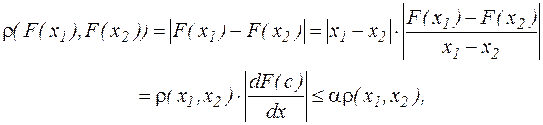
где 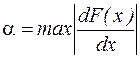 .
.
Отсюда вытекает следующее утверждение.
Если 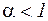 или то же или то же 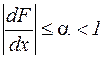 для для 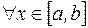 , то отображение , то отображение 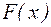 является сжимающим. Следовательно, итерационный процесс в этом случае сходится. является сжимающим. Следовательно, итерационный процесс в этом случае сходится.
|
Погрешность n -го приближения определяется соотношением (3.10).
Остановимся в заключение на процедуре приведения уравнения (4.1) к виду (4.5). Один из её вариантов состоит в следующем:
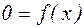 - исходное уравнение;
- исходное уравнение;
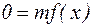 - где m, - подлежащий определению параметр;
- где m, - подлежащий определению параметр;
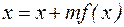 - новая форма уравнения;
- новая форма уравнения;
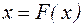 , где
, где 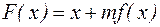 - требуемая форма.
- требуемая форма.
Наконец, значение параметра m выбирается из условия
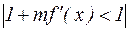
для 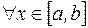 .
.
 2015-06-24
2015-06-24 311
311








