1. Путем ручного просчета найти корень заданного уравнения двумя методами (из четырех рассмотренных) с заданной точностью. Отделение корней провести графически. Привести все необходимые промежуточные вычисления. Результаты свести в итоговую таблицу:
| № итерации | Xn | |Xn-Xn-1| или |Bn-An| | F(Xn) |
Замечание. Для каждого уравнения необходимо найти один корень. Если уравнение имеет более одного корня, необходимо отыскать ближайший к началу координат.
Номер уравнения выбрать по формуле: k+21*(q-1).
Здесь k – номер студента в списке группы; q=1 для группы А и 2 для группы Б.
Допустимая погрешность вычисляется по формуле:
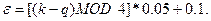
Номера применяемых методов (1-дихотомии; 2-хорд; 3-касательных; 4-простой итерации) вычислить по формуле:
N1=(k-q)MOD 2+1; (первый метод)
N2=[(k+q)DIV 2]MOD 2+3 (второй метод).
Варианты к заданию
1. 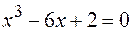 .
.
2. 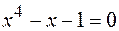 .
.
3. 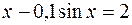 .
.
4. 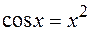 .
.
5. 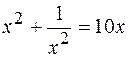 .
.
6. 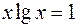 .
.
7. 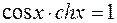 .
.
8. 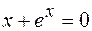 .
.
9. 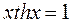 .
.
10. 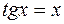 .
.
11. 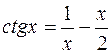 .
.
12. 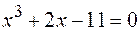 .
.
13. 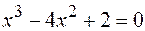 .
.
14. 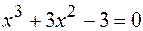 .
.
15. 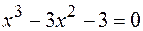 .
.
16. 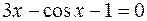 .
.
17. 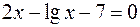 .
.
18. 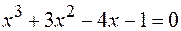 .
.
19. 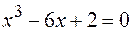 .
.
20. 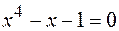 .
.
21. 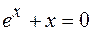 .
.
22. 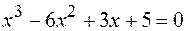 .
.
23. 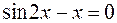 .
.
24. 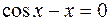 .
.
25. 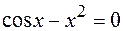 .
.
26. 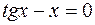 .
.
27. 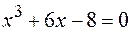 .
.
28. 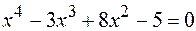 .
.
29. 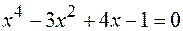 .
.
30. 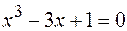 .
.
31. 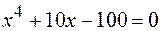 .
.
32. 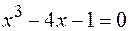 .
.
33. 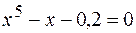 .
.
34. 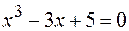 .
.
35. 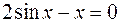 .
.
36. 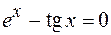 .
.
37. 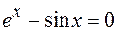 .
.
38. 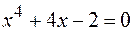 .
.
39. 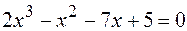 .
.
40. 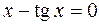 .
.
41. 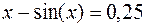
42. 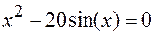
43. 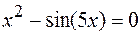
44. 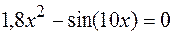
45. 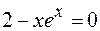
 2015-06-24
2015-06-24 522
522








