Задача 1
Z 3 = { 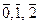 }, Z 4 = {
}, Z 4 = { 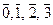 }. Найти Z3*
}. Найти Z3*  Z4*,построить таблицу Кэли для умножения Z3*
Z4*,построить таблицу Кэли для умножения Z3*  Z4*. Является ли Z3*
Z4*. Является ли Z3*  Z4* абелевой группой? Какой мультипликативной группе классов вычетов она изоморфна?
Z4* абелевой группой? Какой мультипликативной группе классов вычетов она изоморфна?
Решение. 1) Построим таблицу Кэли по сложению для групп Z 3 = { 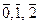 },
},
| + | 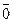 |  |  |
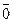 | 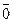 |  |  |
 |  |  | 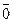 |
 |  | 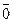 |  |
Z 4 = { 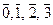 }
}
| + | 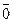 |  |  |  |
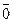 | 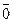 |  |  |  |
 |  |  |  | 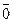 |
 |  |  | 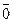 |  |
 |  | 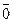 |  |  |
2) Z 3* = { 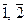 }, Z 4 * = {
}, Z 4 * = { 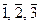 }. Умножение в Z 3* и в Z 4 * зададим таблицами Кэли
}. Умножение в Z 3* и в Z 4 * зададим таблицами Кэли
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
 |  |  |
3) Прямое произведение групп Z 3*  Z 4 * ={(
Z 4 * ={( ,
,  ),(
),( ,
,  ),(
),( ,
,  ),(
),( ,
,  )}
)}
 | ( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) |
( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) |
( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) |
( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) |
( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) | ( , ,  ) ) |
4) Элементы таблицы, симметричные относительно диагонали, совпадают, поэтому группа Z 3*  Z 4* является абелевой.
Z 4* является абелевой.
5) Из теории известно, что если (m, n) = 1, то Z m*  Z n*
Z n* 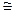 Z mn*. Поэтому имеем: (3, 4) = 1
Z mn*. Поэтому имеем: (3, 4) = 1 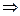 Z 3*
Z 3*  Z 4 *
Z 4 * 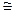 Z 12*= {
Z 12*= {  ,
, 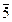 ,
, 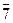 ,
, 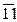 }.
}.
Итак, Z 3*  Z 4 *
Z 4 * 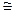 Z 12*= {
Z 12*= {  ,
, 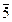 ,
, 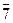 ,
, 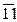 }.
}.
 2015-06-24
2015-06-24 2612
2612








