Найти порядок группы Z 5*  Z 12 *.
Z 12 *.
Решение. Так как 5 и 12 взаимно простые числа то порядок прямого произведения групп можно вычислить, используя функцию Эйлера. (Если (m, n) = 1, то Z m*  Z n *
Z n * 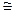 Z mn*)
Z mn*)
(5, 12) = 1 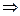 Z 5*
Z 5*  Z 12 *
Z 12 * 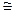 Z 60*
Z 60* 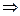 | Z 5*
| Z 5*  Z 12 * |
Z 12 * | 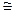 | Z 60*|=
| Z 60*|=  ( 60 ) = 16
( 60 ) = 16
Ответ: порядок группы Z 5*  Z 12 * равен 16.
Z 12 * равен 16.
Задача 3
Вычислить: а)  -1 в Z 7, Z 7 = {
-1 в Z 7, Z 7 = { 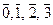 ,
, 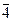 ,
, 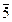 ,
, 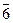 }, (
}, ( )-1=
)-1= 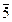 , так как
, так как  ×
× 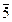 =
= 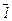 ;
;
б) 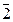 -1 в Z 5, Z 5 = {
-1 в Z 5, Z 5 = { 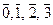 ,
, 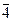 ,
, 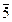 }, (
}, (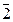 )-1=
)-1=  ;
;
в) 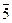 -1 в Z 13, Z 13 = {
-1 в Z 13, Z 13 = { 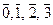 ,…,
,…, 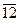 }, (
}, (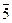 )-1 =
)-1 = 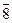 .
.
Задача 4
Вычислить класс 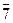 -1 в Z 11 с помощью теоремы Эйлера.
-1 в Z 11 с помощью теоремы Эйлера.
Решение. Теорема Эйлера, если (a, m)  1, то a
1, то a 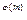
 1(m) или (
1(m) или ( , m)
, m)  1, (
1, ( )
) 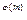

 (mod m)
(mod m)
(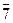 , 11)
, 11)  1, поэтому 7
1, поэтому 7 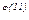
 1(11) или 7
1(11) или 7 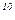
 1(11). Тогда 7
1(11). Тогда 7 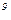 ×7
×7  1(11), поэтому
1(11), поэтому 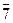 -1 = (
-1 = (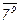 ). 79 = (72)4 × 7
). 79 = (72)4 × 7  54 × 7
54 × 7  (25)2 × 7
(25)2 × 7  (3)2 × 7
(3)2 × 7  9 × 7
9 × 7  63
63  8 (11).
8 (11). 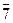 -1 =
-1 = 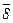 .
.
 2015-06-24
2015-06-24 2086
2086








