2015-06-24
394
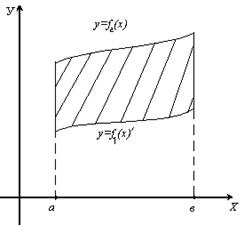
Используя геометрический смысл определенного интеграла, нетрудно получить формулу для вычисления площади плоской фигуры, ограниченной кривыми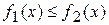 
и прямыми 
:
.
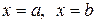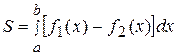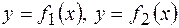
Пример 32
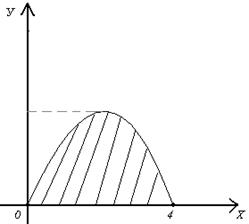
Вычислить площадь фигуры, ограниченной параболой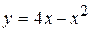 
и осью 
.
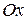Решение.
Парабола пересекает ось 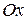в точках 
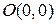и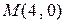 
,
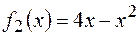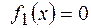.Поэтому: 
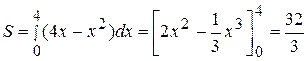(кв.ед.).
Вычисление объемов тел вращения
При вращении криволинейной трапеции, ограниченной линиями: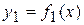 
, 
, 
; 
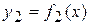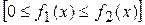
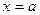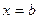вокруг оси 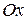, получим объем тела вращения:
.
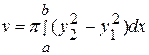Пример 33
Найти объем тела, образованного вращением вокруг оси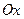 
фигуры, ограниченной кривой 
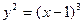и прямой 
.
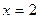Решение.
Для построения кривой найдем точки:
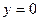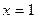при 
, 
; при ,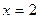 
.
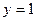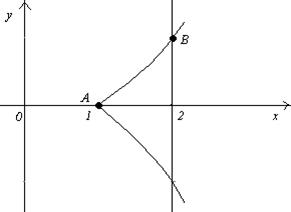
А(1,0); В(2,1)
