1) 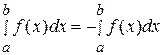 ; 2)
; 2) 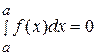 ;
;
3) 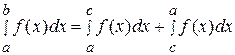 ;
;
4) 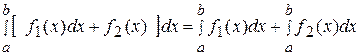 ;
;
5) 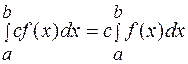 , где
, где 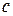 - постоянная.
- постоянная.
Правила вычисления определенного интеграла
1) Формула Ньютона-Лейбница:
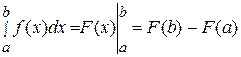 ,
,
где 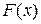 - первообразная для
- первообразная для 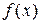 .
.
2) Интегрирование по частям:
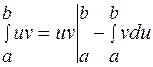 ,
,
где 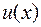 и
и 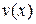 - непрерывные и дифференцируемые функции на отрезке
- непрерывные и дифференцируемые функции на отрезке 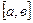 .
.
3) Замена переменной:
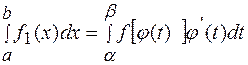 ,
,
где 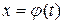 - функция, непрерывная вместе со своей производной
- функция, непрерывная вместе со своей производной 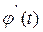 на отрезке
на отрезке 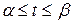 .
.
4) 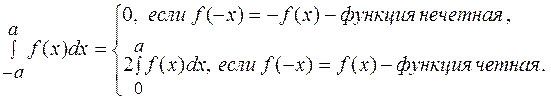
Пример 29 Вычислить:
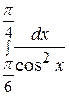 .
.
Решение.
По формуле Ньютона-Лейбница будем иметь:
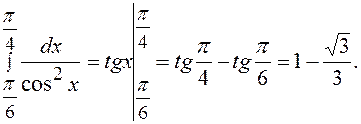
Пример 30. Вычислить:
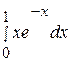 .
.
Решение.
Используем формулу интегрирования по частям:
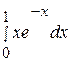 =
= 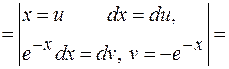
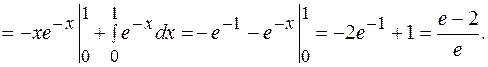
Пример 31 Вычислить:
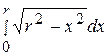 .
.
Решение.
Сделаем замену переменной: 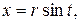
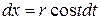 ;
; 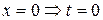 ;
; 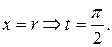
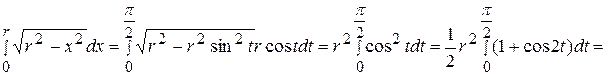
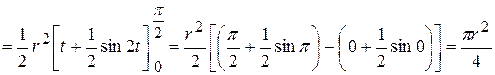 .
.
Приложения определенного интеграла
 2015-06-24
2015-06-24 288
288








