1. а) 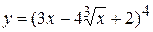 , б)
, б) 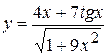 ,
,
в) 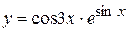 , г)
, г) 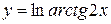 ,
,
д) 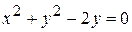 .
.
2. а) 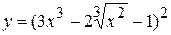 , б)
, б) 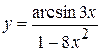 ,
,
в) 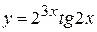 , г)
, г) 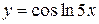 ,
,
д) 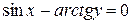 .
.
3. а) 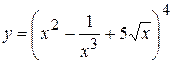 , б)
, б) 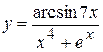 ,
,
в) 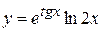 , г)
, г) 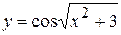 .
.
д) 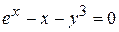 .
.
4. а) 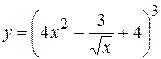 , б)
, б) 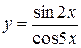 ,
,
в) 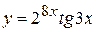 , г)
, г) 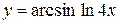 ,
,
д) 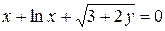 .
.
5. а) 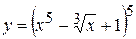 , б)
, б) 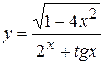 ,
,
в) 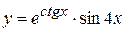 , г)
, г) 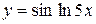 ,
,
д) 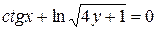 .
.
6. а) 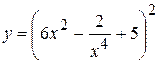 , б)
, б) 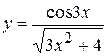 ,
,
в) 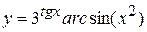 , г)
, г) 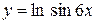 ,
,
д) 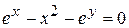 .
.
7. а) 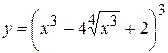 , б)
, б) 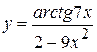 ,
,
в) 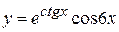 , г)
, г) 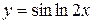 ,
,
д) 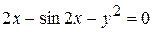 .
.
8. а) 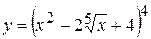 , б)
, б) 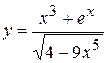 ,
,
в) 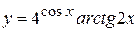 , г)
, г) 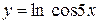 ,
,
д) 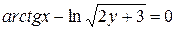 .
.
9. а) 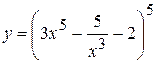 , б)
, б) 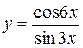 ,
,
в) 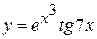 , г)
, г) 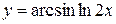 ,
,
д) 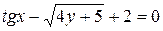 .
.
10. а) 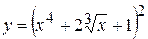 , б)
, б) 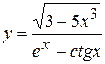 ,
,
в) 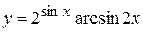 , г)
, г) 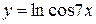 ,
,
д) 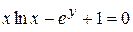 .
.
11. а) 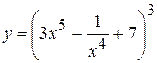 , б)
, б) 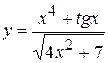 ,
,
в) 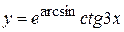 , г)
, г) 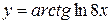 ,
,
д) 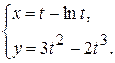
12. а) 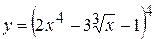 , б)
, б) 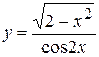 ,
,
в) 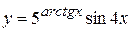 , г)
, г) 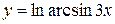 ,
,
д) 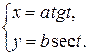
13. а) 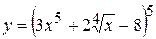 , б)
, б) 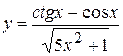 ,
,
в) 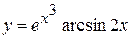 , г)
, г) 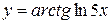 ,
,
д) 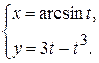
14. а) 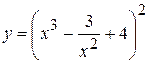 , б)
, б) 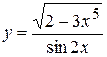 ,
,
в) 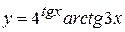 , г)
, г) 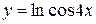 ,
,
д) 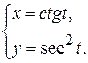
15. а) 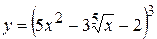 , б)
, б) 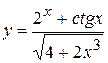 ,
,
в) 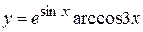 , г)
, г) 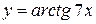 ,
,
д) 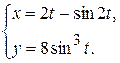
16. а) 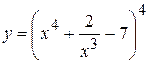 , б)
, б) 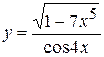 ,
,
в) 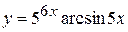 , г)
, г) 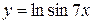 ,
,
д) 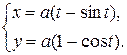
17. а) 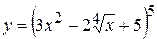 , б)
, б) 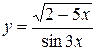 ,
,
в) 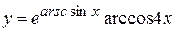 , г)
, г) 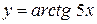 ,
,
д) 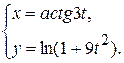
18. а) 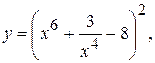 б)
б) 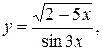
в) 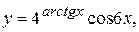 г)
г) 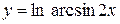 ,
,
д) 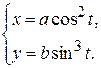
19. а) 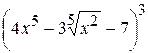 , б)
, б) 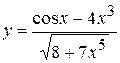 ,
,
в) 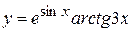 , г)
, г) 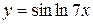 ,
,
д) 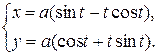
20. а) 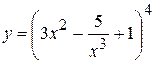 , б)
, б) 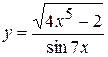 ,
,
в) 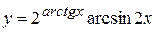 , г)
, г) 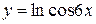 ,
,
д) 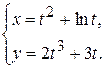
Задача №2
Исследовать функцию методами дифференциального исчисления и построить ее графики:
1. 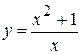 . 7.
. 7. 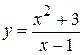 . 14.
. 14. 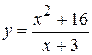 .
.
2. 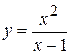 . 8.
. 8. 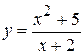 . 15.
. 15. 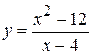 .
.
3. 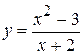 . 9.
. 9. 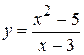 . 16.
. 16. 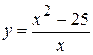 .
.
4. 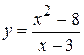 . 10.
. 10. 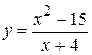 . 17.
. 17. 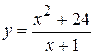 .
.
5. 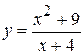 . 11.
. 11. 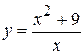 . 18.
. 18. 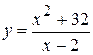 .
.
6. 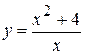 . 12.
. 12. 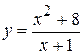 . 19.
. 19. 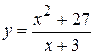 .
.
13. 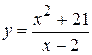 . 20.
. 20. 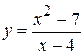 .
.
Задача №3
Найти неопределенные интегралы способом подстановки (методом замены переменного).
1. 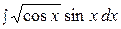 7.
7. 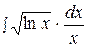 14.
14. 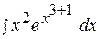
2. 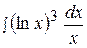 8.
8. 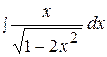 15.
15. 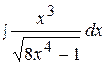
3. 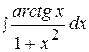 9.
9. 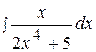 16.
16. 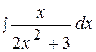
4. 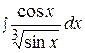 10.
10. 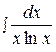 17.
17. 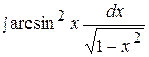
5. 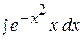 11.
11. 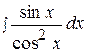 18.
18. 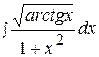
6. 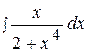 12.
12. 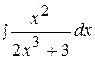 19.
19. 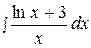
13. 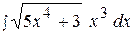 20.
20. 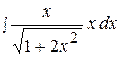
Задача №4
Найти неопределенные интегралы, используя выделение полного квадрата.
1. 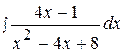
 11.
11. 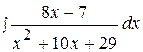
2. 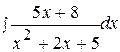 12.
12. 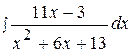
3. 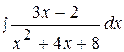 13.
13. 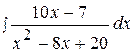
4. 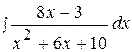 14.
14. 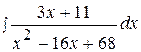
5. 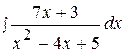 15.
15. 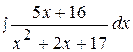
6. 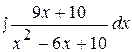 16.
16. 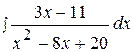
7. 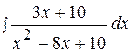 17.
17. 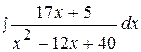
8. 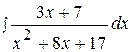 18.
18. 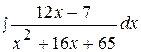
9. 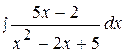 19.
19. 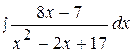
10. 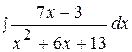 20.
20. 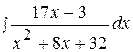
Задача №5
Найти неопределенные интегралы, применяя метод интегрирования по частям.
1. 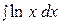
 11.
11. 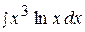
2. 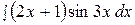 12.
12. 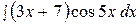
3. 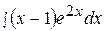 13.
13. 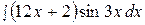
4. 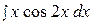 14.
14. 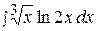
5. 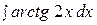 15.
15. 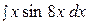
6. 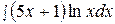 16.
16. 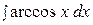
7. 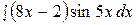 17.
17. 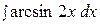
8. 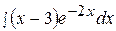 18.
18. 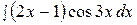
9. 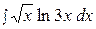 19.
19. 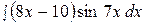
10. 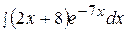 20.
20. 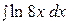
Задача №6
Найти неопределенные интегралы, пользуясь разложением рациональных дробей на простейшие.
1. 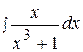
 11.
11. 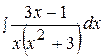
2. 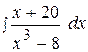 12.
12. 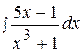
3. 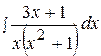 13.
13. 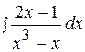
4. 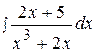 14.
14. 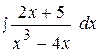
5. 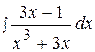 15.
15. 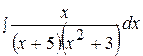
6. 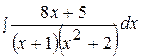 16.
16. 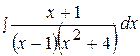
7. 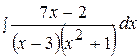 17.
17. 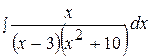
8. 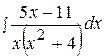 18.
18. 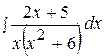
9. 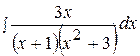 19.
19. 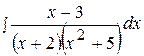
10. 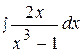 20.
20. 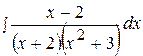
 2015-06-24
2015-06-24 428
428








