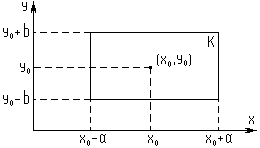 Рассмотрим функцию
Рассмотрим функцию 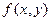 , определенную и непрерывную в прямоугольнике К:
, определенную и непрерывную в прямоугольнике К: 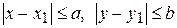
Определение. Если для любого 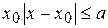 и любых двух значений
и любых двух значений 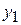 и
и 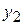 переменной
переменной 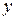 :
:
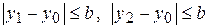 , существует такое, не зависящее от х число
, существует такое, не зависящее от х число 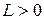 , что выполнено неравенство:
, что выполнено неравенство: 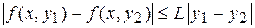 (1), то говорят, что функция
(1), то говорят, что функция 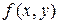 в области К удовлетворяет условию Липшица с постоянной L.
в области К удовлетворяет условию Липшица с постоянной L.
Замечания:
1. Если 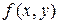 в области К имеет непрерывную частную производную
в области К имеет непрерывную частную производную 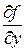 , то всегда найдется такое L, что условие (1) будет выполнено. Действительно, тогда по формуле Лагранжа
, то всегда найдется такое L, что условие (1) будет выполнено. Действительно, тогда по формуле Лагранжа 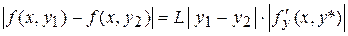 (2),
(2),
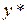 – лежит между
– лежит между 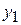 и
и 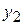 .
.
В силу непрерывности 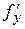 в К и замкнутости области К,
в К и замкнутости области К, 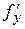 в К ограничена, т.е.
в К ограничена, т.е. 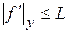 , где L – некоторая константа. В этом случае, в частности, за L можно принять
, где L – некоторая константа. В этом случае, в частности, за L можно принять 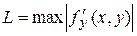 .
.
2. Условие Липшица (1) более слабое, чем существование частной производной 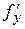 , так как оно может быть выполнено и в том случае, когда
, так как оно может быть выполнено и в том случае, когда 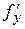 существует не всюду в К.
существует не всюду в К.
Примеры:
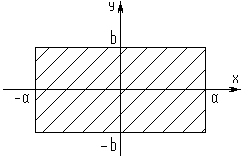
1. Определить, удовлетворяет ли условию Липшица функция 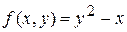 заданная в прямоугольнике
заданная в прямоугольнике 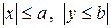 ?
?
 |
Решение.
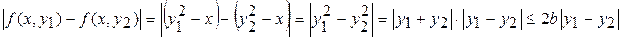
Следовательно, за L можно принять 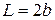 и условие Липшица выполнено. Тот же результат получим, если используем замечание 1. Действительно, функция
и условие Липшица выполнено. Тот же результат получим, если используем замечание 1. Действительно, функция 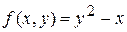 имеет непрерывную
имеет непрерывную 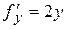 , поэтому за L можно принять
, поэтому за L можно принять 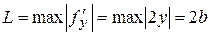 .
.
Таким образом, заданная функция удовлетворяет условию Липшица в любом конечном прямоугольнике.
2. То же самое для функции 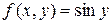 .
.
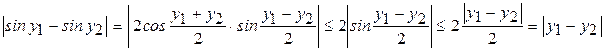
Это значит, что в прямоугольнике K условие выполнено с 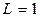 .
.
Здесь константа L не зависит от размеров прямоугольника, следовательно, условие Липшица удовлетворяется на всей плоскости.
3. То же для функции 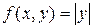
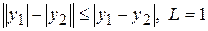
В то же время 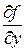 не существует при
не существует при 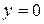 , т.к.
, т.к.
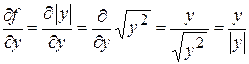 .
.
 2015-06-24
2015-06-24 5097
5097








