Частные случаи уравнений II порядка

Рассмотрим частные случаи уравнений II порядка, допускающих «понижение» порядка, т.е. случаи, когда уравнение II порядка приводится к интегрированию двух уравнений первого порядка.

1. Правая часть не содержит 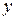и

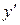
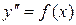(1)

Положим 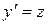. Тогда 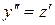и .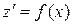

Получили уравнение первого порядка.

Отсюда 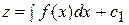или .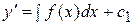

Имеем опять уравнение первого порядка 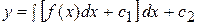или

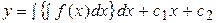
Получили общее решение уравнения (1).

2. Правая часть уравнения не содержит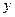

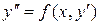(2)

Положим 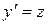, тогда для z имеем уравнение .

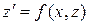Пусть его решение будет 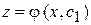. Следовательно, .

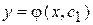Отсюда .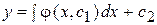

Это общее решение уравнения (2).

Пример. .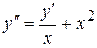

Положим 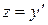, тогда 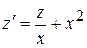и его решение .

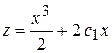Следовательно, 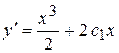и

и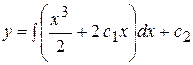ли 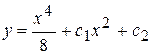– общее решение уравнения (2)

3. Правая часть не содержит х

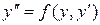(3)

Положим 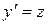и будем считать z функцией y.

Тогда 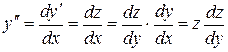. Итак, .

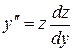Подставляя это в уравнение (3), получим: 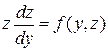, т.е. уравнение первого порядка относительно z. Решив его, будем иметь 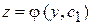или .

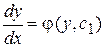Получили уравнение с разделяющимися переменными. Отсюда .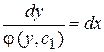

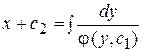Это общий интеграл уравнения (3).

Пример. .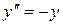

Положим 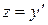, тогда 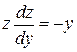или 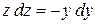. Отсюда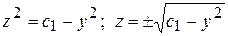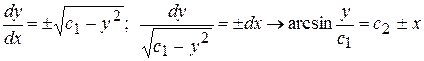

или или 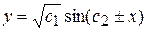- общее решение.