Теорема существования и единственности

Теорема (Коши)

Пусть 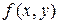удовлетворяет условиям:

1) непрерывна в прямоугольнике K: 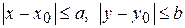, тогда в K 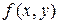ограничена, то найдется такое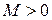 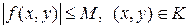(3)

2) удовлетворяет в K условию Липшица

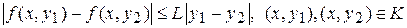(4)

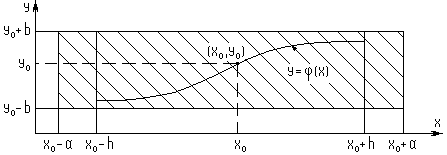
Тогда в интервале: 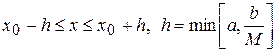(5)

дифференциальное уравнение 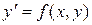(6)

обладает единственным решением 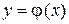, таким, что .

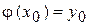Замечания:

1. Для существования решения достаточно непрерывности 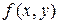в K.

2. Для единственности решения требуется выполнение условия Липшица (4), которое может быть заменено более жестким условием существования в K непрерывной .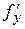

3. При доказательстве теоремы рассматривается задача Коши: 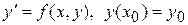, (7)

которая заменяется эквивалентным ей интегральным уравнением 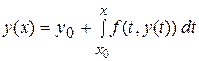. (8)

Затем к уравнению (8) применяется так называемый метод последовательных приближений Пикара. Он состоит в том, что строится последовательность функций 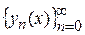сходящаяся к решению уравнения (8). Функции 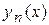строятся по следующему правилу: за исходное приближение принимается 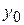, а следующие вычисляются по формуле: 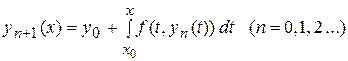. (9)

Это есть рабочая формула для построения приближенного решения по методу последовательных приближений.

4. 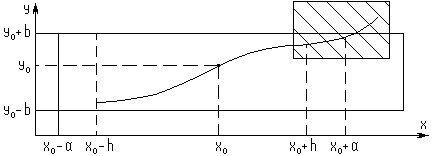Допустим интегральная кривая построена на интервале 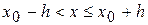. Возьмем конечную точку за центр нового прямоугольника и продолжим решение вправо. Поступая так, каждый раз, можно продолжить решение (интегральную кривую) до самой границы области G задания функции 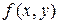(в предположении, что G конечна и замкнута).

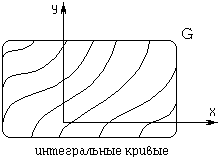
Мы построили интегральную кривую, проходящую через точку 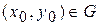. Можно выбрать любую другую точку и опять получим единственную интегральную кривую. Таким образом, область G как бы состоит из интегральных кривых.

Теорема. Если 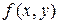определена и непрерывна на всей плоскости и удовлетворяет условию Липшица во всякой конечной области этой плоскости, то всякая интегральная кривая при возрастании или продолжима до 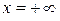или имеет вертикальную асимптоту при конечном значении 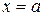, т.е. интегральная кривая не может окончится где-то внутри области.

Пример. .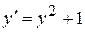

Здесь 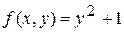удовлетворяет всем условиям теоремы. Решением задачи Коши 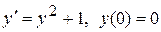будет 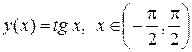. Решение имеет вертикальные асимптоты .

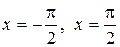5. Те точки области G, в которых функция 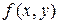неопределена или перестает быть непрерывной или не выполняется условие Липшица, называются особыми точками уравнения 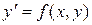. Таким образом, особые точки это те точки, в которых нарушаются условия теоремы существования и единственности. Особые точки могут быть изолированными, а могут составлять и целые области.