Рассмотрим функцию: 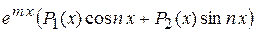 , (4)
, (4)
где 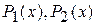 – полиномы, а числа m и n – вещественные любые.
– полиномы, а числа m и n – вещественные любые.
По виду этой функции составим «контрольное число» 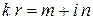 .
.
Пусть корни характеристического уравнения будут 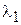 и
и 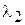 .
.
Определим число k следующим образом:
1) 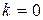 , если контрольное число не совпадает ни с одним из корней
, если контрольное число не совпадает ни с одним из корней 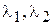 ;
;
2) 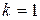 , если
, если 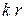 совпадает с одним из корней
совпадает с одним из корней 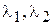 ;
;
3) 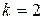 , если
, если 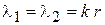 .
.
Правило. Если правая часть уравнения (1) имеет вид:
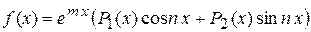 (5),
(5),
то частное решение следует искать в форме
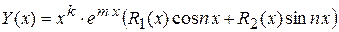 (6),
(6),
где 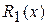 и
и 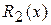 – полиномы степени, равной наивысшей из степеней полиномов
– полиномы степени, равной наивысшей из степеней полиномов 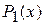 и
и 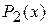 .
.
Схема нахождения 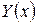 :
:
1) зная вид 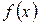 , записывают
, записывают 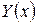 в форме (3), причем полиномы и
в форме (3), причем полиномы и 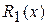 и
и 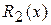 записываются с неопределенными коэффициентами;
записываются с неопределенными коэффициентами;
2) подставляют 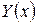 в уравнение (1) вместо y, и приравнивают коэффициенты при одинаковых функциях справа и слева. Получают систему уравнений для коэффициентов многочленов
в уравнение (1) вместо y, и приравнивают коэффициенты при одинаковых функциях справа и слева. Получают систему уравнений для коэффициентов многочленов 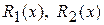 . Решая эту систему, находят неизвестные коэффициенты.
. Решая эту систему, находят неизвестные коэффициенты.
3) Найденные коэффициенты подставляют в формулу (3) и находят 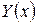 .
.
Замечания:
1. Если функция имеет вид: 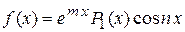 или
или 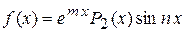

, то частное решение 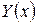 все равно ищется в виде (6)
все равно ищется в виде (6) 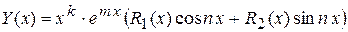 .
.
2. Если 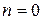 , то
, то 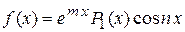 . В этом случае частное решение ищется в форме:
. В этом случае частное решение ищется в форме: 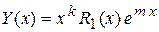 . При этом степень
. При этом степень 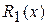 равна степени
равна степени 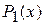 и
и 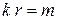 .
.
3. Если 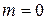 , то
, то 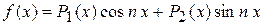 , а
, а 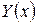 имеет вид
имеет вид 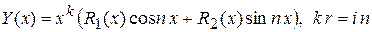 .
.
Пример. 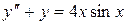
Здесь: 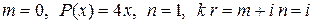
Характеристическое уравнение 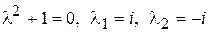 . Следовательно,
. Следовательно, 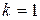 .
.
Поэтому 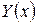 следует искать в виде:
следует искать в виде: 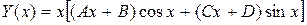
Отсюда 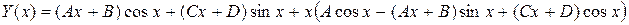
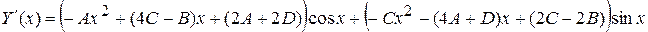 Подставляя в уравнение
Подставляя в уравнение 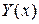 и
и 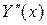 , находим:
, находим:
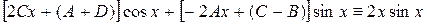
Отсюда 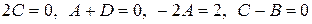 или
или
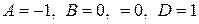 .
.
Следовательно, 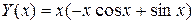 .
.
 2015-06-24
2015-06-24 742
742








