Линейное неоднородное уравнение с постоянными коэффициентами

Рассмотрим линейное неоднородное уравнение

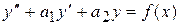, (1)

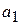где и 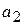– заданные постоянные коэффициенты.

Нам уже известно, что общее решение такого уравнения складывается из общего решения 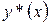, соответствующего однородного уравнения

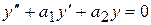(2)

и какого-нибудь частного решения 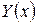уравнения (1), т.е. 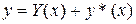. (3)

Как строить общее решение 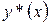однородного уравнения (2), мы рассмотрим в предыдущем параграфе. Поэтому теперь вопрос об общем решении уравнения (1) сведен лишь к вопросу о построении хотя бы какого-нибудь частного решения 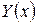уравнения (1). Вообще говоря, 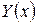можно, например, угадать. Но такой способ определения 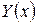очень ненадежен. Мы укажем сейчас точные способы, которые всегда приводят к цели.