Наименование занятия: Действия над комплексными числами в тригонометрической и показательной формах.
Цель занятия: Научиться выполнять действия над комплексными числами.
Подготовка к занятию: Повторить теоретический материал по теме «Комплексные числа».
Литература:
- Григорьев В.П., Дубинский Ю.А. «Элементы высшей математики», 2008г.
Задание на занятие:
- Даны комплексные числа
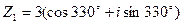 и
и 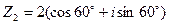 . Найти: Z 1· Z 2,
. Найти: Z 1· Z 2, 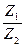 , (Z 2)4,
, (Z 2)4, 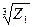 .
. - Записать комплексные числа в тригонометрической и показательной формах.
1) Z = 5 i;
2) Z = -2 – 2 i;
3) Z = 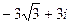 ;
;
4) Z = -6.
- Записать комплексные числа в алгебраической и показательной формах.
1) 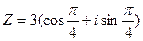 ;
;
2) 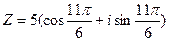 ;
;
3) 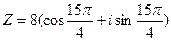 ;
;
4) 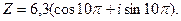
- Записать комплексные числа в алгебраической и тригонометрической формах.
1) 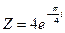 ;
;
2) 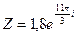 ;
;
- Выполнить действия, используя показательную форму комплексного числа:
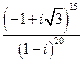
- Решить уравнения:
1) z 4 = i;
2) z4 + z 2 + 1 = 0.
Порядок проведения занятия:
- Получить допуск к работе
- Выполнить задания
- Ответить на контрольные вопросы.
Содержание отчета:
- Наименование, цель занятия, задание;
- Выполненное задание;
- Ответы на контрольные вопросы.
Контрольные вопросы для зачета:
- Что называется модулем и аргументом комплексного числа? Как они вычисляются?
- Как записывается комплексное число в тригонометрической, показательной формах?
- Как найти произведение и частное комплексных чисел, записанных в тригонометрической, показательной формах?
- Как возвести в степень число, записанное в тригонометрической, показательной формах?
- Сколько значений имеет корень n -й степени, записанное в тригонометрической, показательной формах?
ПРИЛОЖЕНИЕ
Тригонометрическая форма комплексного числа 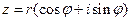
Показательная форма комплексного числа 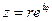
Величина r называется модулем комплексного числа, а угол наклона j - аргументом комплексного числа. 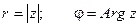 ;
; 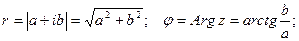
 2015-06-24
2015-06-24 418
418








