Пусть комплексные числа 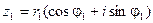 ,
, 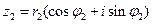 записаны в тригонометрической форме и
записаны в тригонометрической форме и 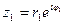 ,
, 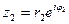 - в показательной.
- в показательной.
В тригонометрической и показательной формах удобно производить следующие действия:
1. Умножение: 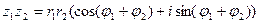 ;
; 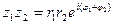
2. Деление: 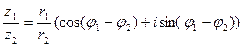 ;
; 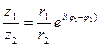
3. Возведение в степень: 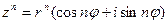 ;
; 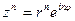 , где n – натуральное число.
, где n – натуральное число.
4. Извлечение корня из комплексного числа:
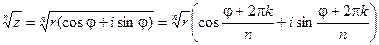 ;
; 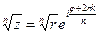
Корень n – ой степени из комплексного числа имеет n различных значений.
Пример. Число 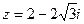 записать в тригонометрической форме, найти z20,
записать в тригонометрической форме, найти z20, 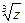
Число 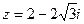 представим в тригонометрической форме.
представим в тригонометрической форме.
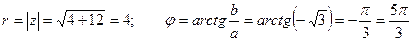 . Тогда
. Тогда 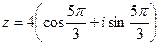 .
.
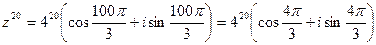
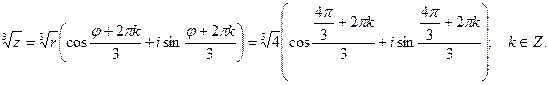
При k = 0 получим 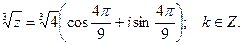
При k = 1 получим 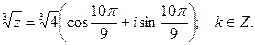
При k = 2 получим 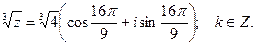
При k = 3 получим 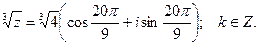
 2015-06-24
2015-06-24 454
454








