Предел отношения двух бесконечно малых (Правило Лопиталя)

Дополнение к правилам предельного перехода.

Теорема. ( Правило Лопиталя) .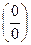

Пусть 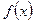и 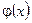на отрезке 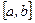удовлетворяет условиям теоремы Коши и .

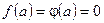Тогда пусть $ 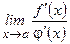, то $ .

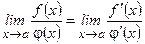Доказательство.

Пусть .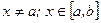

Применяем теорему Коши 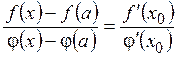, где .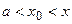

Т.к. по условию ,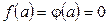

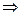
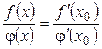т.к. 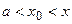, то при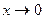 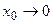; при этом, если 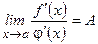, то .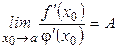

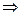
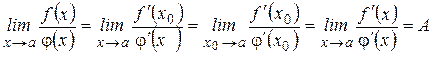Примеры (стр. 6) № 1, 2.

1. Теорема имеет силу и в том случае, есл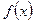и и 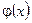не определены при 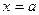, но 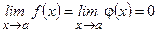. (Просто доопределяем функции .)

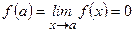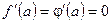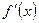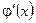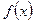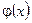2. Если и функции и удовлетворяют условиям теоремы для и , то применяем правило Лопиталя к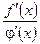 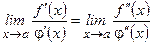и т. д. (Пример № 3).

3. Если 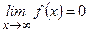, 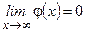- правило Лопиталя применимо: пусть 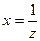(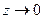при ) ,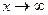

.

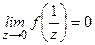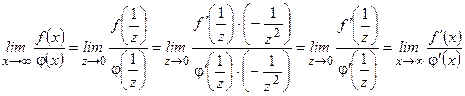Теорема 2. Пусть 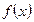и 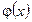непрерывны и дифференцируемы в окрестности точк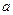и при 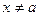. 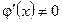и пусть 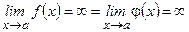, то $ $ .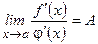

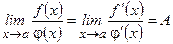(Без доказательства).

Примеры.

1.

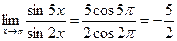
2.

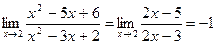
3.

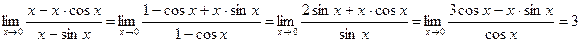
4.

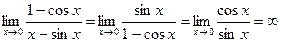
5. 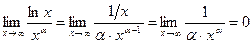, a>0

6. Не берется по правилу Лопиталя.

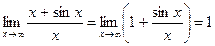
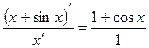® колеблется на [0,2]