2.
1.
Т.1.4.Основные теоремы дифференциального исчисления. Правило Лопиталя, 4ч.
План
1.Теоремы о дифференцируемых функциях.
2.Правило Лопиталя.
3.Геометрический смысл теорем дифференциального исчисления.
Теорема Ферма. Если дифференцируемая на промежутке X функция у = f(x) достигает наибольшего или наименьшего значения во внутренней точке х0 этого промежутка, то производная функция в этой точке равна нулю, т.е. f'(х0) = 0.

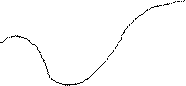
 F'(x0) = 0
F'(x0) = 0
 | |||
 | |||
 | |||
 | |||
 | |||


 хo
хo



 X
X
Теорема Ролля. Пусть функция y = f(x) удовлетворяет следующие условиям:
1. непрерывна на отрезке 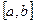 ;
;
2. дифференцируема на интервале 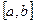 ;
;
3. на концаx отрезка принимает равные значение, т.е. f(a) = f(b).
Тогда внутри отрезка существует по крайней мере одна такая точка ξє (а, b), в которой производная функция равна нулю: f'( ξ ) = 0.
Теорема Лагранжа. Пусть функция y = f(x) удовлетворяет следующим условиям:
1. непрерывная на отрезке 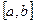 ;
;
2. дифференцируема на интервале 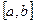 ;
;
Тогда внутри отрезка существует по крайней мере одна такая точка ξє (а, b), в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке, т.е.
f'( ξ ) = 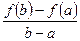 .
.
Теорема. Предел отношения двух бесконечно малыx или бесконечно больших функций равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле.
Итак, если имеется неопределенность вида 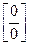 или
или 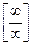 , то
, то
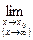
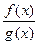 =
= 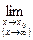
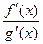 .
.
С.Р. 1.Геометрический смысл теоремы Лагранжа.
2.Доказательство теоремы Ферма.
3.Повторное применение правила Лопиталя.
 2014-02-09
2014-02-09 1077
1077








