Правило Лопиталя. Предел отношения двух дифференцируемых или бесконечно малых или бесконечно больших функций при 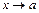 (
(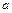 - число
- число 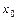 или символ
или символ 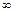 ) равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле:
) равен пределу отношения их производных (конечному или бесконечному), если последний существует в указанном смысле: 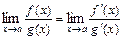 . Правило Лопиталя используют для раскрытия неопределённостей видов
. Правило Лопиталя используют для раскрытия неопределённостей видов 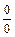 и
и 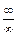 .
.
На каждом этапе применения правила Лопиталя следует пользоваться упрощающими отношение тождественными преобразованиями, а также комбинировать это правило с любыми другими приёмами вычисления пределов. В некоторых случаях может потребоваться неоднократное применение данного правила.
Раскрытие неопределённостей видов 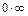 ,
, 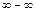 ,
, 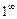 ,
, 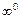 ,
, 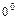 путём преобразований:
путём преобразований:
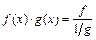 ,
, 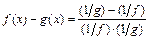 ,
, 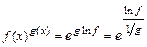
приводится к раскрытию неопределенностей видов 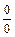 и
и 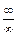 .
.
В задачах 5.171-5.220 вычислить пределы:
5.171 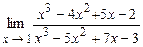 . 5.172
. 5.172 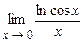 .
.
5.173 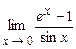 . 5.174
. 5.174 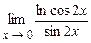 .
.
5.175 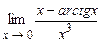 . 5.176
. 5.176 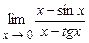 .
.
5.177 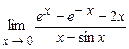 . 5.178
. 5.178 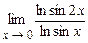 .
.
5.179 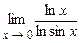 . 5.180
. 5.180 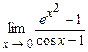 .
.
5.181 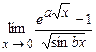 . 5.182
. 5.182 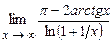 .
.
5.183 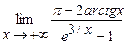 . 5.184
. 5.184 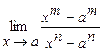 .
.
5.185 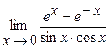 . 5.186
. 5.186 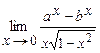 .
.
5.187 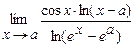 . 5.188
. 5.188 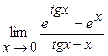 .
.
5.189 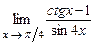 . 5.190.
. 5.190. 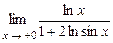 .
.
5.191 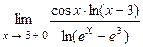 . 5.192
. 5.192 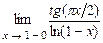 .
.
5.193 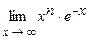 . 5.194
. 5.194 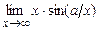 .
.
5.195 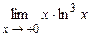 . 5.196
. 5.196 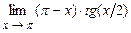 .
.
5.197 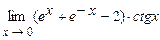 . 5.198
. 5.198 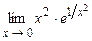 .
.
5.199 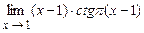 . 5.200
. 5.200 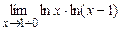 .
.
5.201 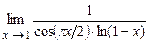 . 5.202
. 5.202 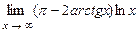 .
.
5.203 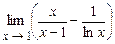 . 5.204
. 5.204 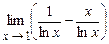 .
.
5.205 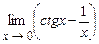 . 5.206
. 5.206 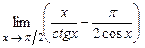 .
.
5.207 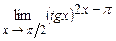 . 5.208
. 5.208 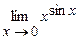 .
.
5.209 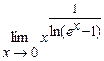 . 5.210
. 5.210 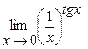 .
.
5.211 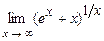 . 5.212
. 5.212 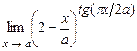 .
.
5.213 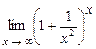 . 5.214
. 5.214 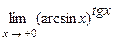 .
.
5.215 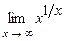 . 5.216
. 5.216 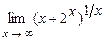 .
.
5.217 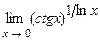 . 5.218
. 5.218 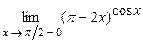 .
.
5.219 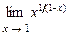 . 5.220
. 5.220 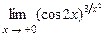 .
.
 2015-03-20
2015-03-20 492
492








