Определение и геометрический смысл смешанного произведения

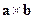Если вектор умножить векторно на и полученный вектор умножить скалярно на вектор 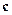, то число, полученное в результате этих умножений, называется смешанным произведением векторов .

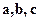Определение. Число, равное 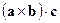, называют смешанным произведением векторов .

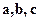Смешанное произведение векторов 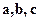обозначается 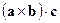или .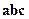

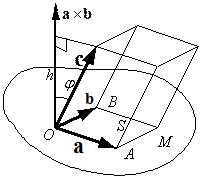На векторах 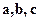, приложенных к общему началу, можно построить параллелепипед (рис. 2.21).
Если векторы 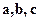образуют правую тройку, то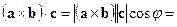 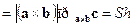, где 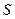- площадь параллелограмма,
Рис. 2.21 построенного на векторах и , а 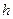высота параллелепипеда, построенного на векторах .

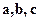Итак, если векторы 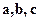образуют правую тройку, то смешанное произведение этих векторов численно равно объёму параллелепипеда, построенного на этих векторах.

Если векторы 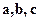образуют левую тройку, то угол между векторам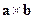и и 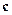тупой и 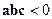, при этом 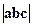равен объёму параллелепипеда, построенного на этих векторах.