2015-06-24
4227
1. С помощью смешанного произведения можно вычислить объём параллелепипеда, построенного на векторах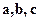 
.
.
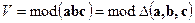Это следует из геометрического смысла смешанного произведения.
Замечание. Объем тетраэдра, построенного на векторах 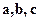, равен 
.
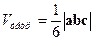2. С помощью смешанного произведения можно установить компланарность трех векторов и их ориентацию.
Три вектора компланарны тогда и только тогда, когда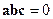 
.
Если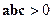 
, то система векторов 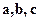правая.
Если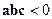 
, то система векторов 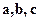левая.
● Пример 18. Проверить, лежат ли точки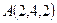 
, 
, 
, 
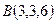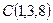в одной плоскости.
Решение. Если указанные точки лежат в одной плоскости, то векторы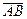 
, 
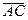и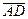 
компланарны. 
, 
, 
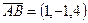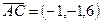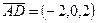. Вычислим смешанное произведение этих векторов.
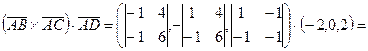
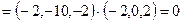. Смешанное произведение равно нулю, поэтому векторы 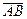, 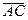и 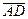компланарны, а данные точки лежат в одной плоскости.●
● Пример 19. Даны вершины тетраэдра: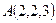 
, 
, 
, 
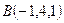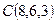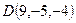. Найти длину высоты тетраэдра, опущенной из вершины 
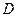(рис.2.22).
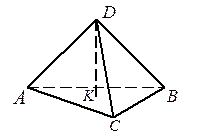Решение. 
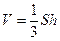, где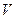 
- объём тетраэдра, 
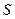- площадь основания 
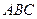, а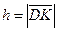 
- искомая высота.
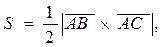
Рис. 2.22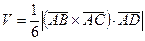 
.
, 
, 
. 
●
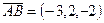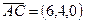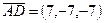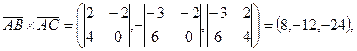
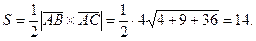
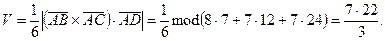
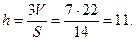● Пример 20. Показать, что векторы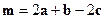 
, 
, 
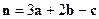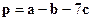компланарны при любых векторах .
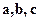Решение. Первый способ. Учитывая свойства векторного и смешанного произведений, вычислим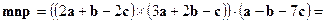 
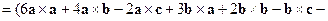
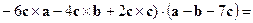
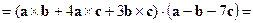
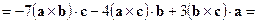
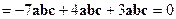. Так как смешанное произведение векторов 
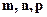равно нулю, то эти векторы компланарны.
