Свойства смешанного произведения. Так как , то свойства смешанного произведения могут быть получены из свойств скалярного произведения и свойств определителя

Так как 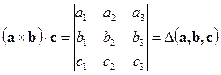, то свойства смешанного произведения могут быть получены из свойств скалярного произведения и свойств определителя.

Свойства смешанного произведения:

а) .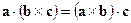

Знаки векторного и скалярного произведений можно переставить местами, но при этом необходимо вначале перемножить соответствующие сомножители векторно.

►Действительно, пользуясь переместительным законом для скалярного произведения и свойствами определителя, имеем ◄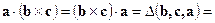

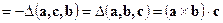б) .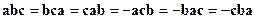

Два сомножителя смешанного произведения можно поменять местами, при этом абсолютное значение смешанного произведения не меняется, а его знак меняется на противоположный.

Докажем, что .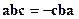

►Действительно, ◄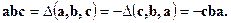

в) Смешанное произведение векторов 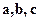равно нулю тогда и только тогда, когда векторы 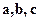компланарны.

Доказательство этого свойстваследует из геометрического смысла смешанного произведения.