2015-06-24
562
Для степенного ряда (2) выполняется одно и только одно из следующих утверждений.
- Ряд (2) сходится только в точке x=0. Такой ряд называют всюду расходящимся.
- Ряд (2) абсолютно сходится на всей числовой оси. Такой ряд называют всюду сходящимся.
- Существует число
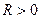, такое, что в интервале 
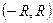ряд (2) абсолютно сходится, а на интервалах 
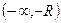и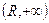 
он расходится.
□
Обозначим M – множество всех точек, в которых ряд (2) сходится.
1. Очевидно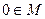 
. Если других точек множество M не имеет, то реализуется первый случай.
2. Предположим теперь, что множество M не ограничено. Тогда для любого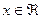 
найдется 
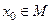, такое, что 
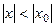и по теореме Абеля ряд сходится абсолютно в любой точке x. Следовательно, выполняется второе утверждение теоремы.
3. Рассмотрим случай, когда множество M содержит точки, отличные от 0 и ограничено. Пусть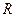 
- число, ограничивающее M: 
.
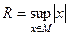Тогда, если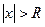 
, то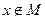 
и ряд (2) расходится в этой точке. Если 
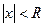, то найдется 
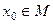, такое, что 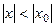и по теореме Абеля ряд сходится абсолютно в точке x. Следовательно, выполняется третье утверждение теоремы.
|
|
|
■
