Пусть ряд (2) сходится в некоторой точке 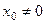 ,тогда ряд (2) сходится абсолютно в любой точке
,тогда ряд (2) сходится абсолютно в любой точке 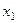 , удовлетворяющей условию
, удовлетворяющей условию 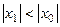 .
.
□
По условию числовой ряд 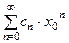 сходится, следовательно, выполняется необходимый признак сходимости
сходится, следовательно, выполняется необходимый признак сходимости 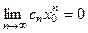 . Но тогда
. Но тогда
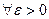 ,
, 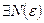 ,
, 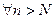
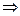
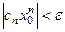 .
.
Отсюда
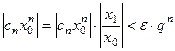 ,
, 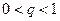 . А так как ряд
. А так как ряд 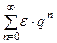 - сходящаяся геометрическая прогрессия, то ряд
- сходящаяся геометрическая прогрессия, то ряд 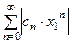 сходится по первому признаку сравнения, т.е. сходится абсолютно ряд
сходится по первому признаку сравнения, т.е. сходится абсолютно ряд 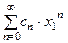 .
.
■
Следствие.
Если степенной ряд (2) расходится в некоторой точке 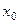 , то он расходится и в любой точке
, то он расходится и в любой точке 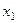 с условием
с условием 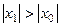 .
.
 2015-06-24
2015-06-24 668
668








