2015-06-24
422
Пусть дан степенной ряд (2) с радиусом сходимости R>0.
Th 1. О равномерной сходимости степенного ряда
Каково бы не было число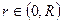 
, то степенной ряд (2) равномерно сходится на любом отрезке 
.
□
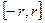Возьмем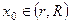 
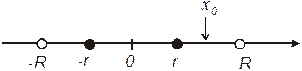. Так как 
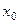принадлежит области сходимости ряда (2), то числовой ряд 
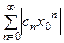сходится, а он является мажорирующим рядом для степенного ряда (2) на отрезке : 
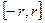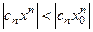при всех 
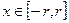. Ряд (2) на отрезке 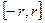сходится равномерно (в силу достаточного признака Вейерштрассе о равномерной сходимости функционального ряда).
■
