Замечание

Число R из третьего утверждения теоремы называется радиусом сходимости степенного ряда, а интервал 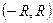- интервалом абсолютной сходимости степенного ряда.

Ради единообразия, понятие радиуса сходимости сохраняется и для других случаев. В первом случае полагают 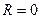, во втором .

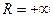Отыскание радиуса сходимости степенного ряда

Пусть дан степенной ряд (2)

Th 1.

Пусть все 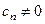, тогда для радиуса сходимости R степенного ряда (2) справедливы формулы

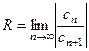, (3)

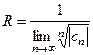, (4)

если эти пределы существуют.

□

Рассмотрим степенной ряд, составленный из модулей

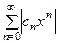(5)

По Th 2 из предыдущего параграфа

при 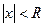ряд сходится, при 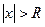- расходится. (6)

Исследуем, ряд (5) с помощью признака Деламбера.

.

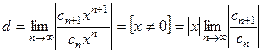Ряд (5) сходится, если 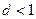, то есть если 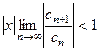, то есть .

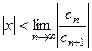Ряд (5) расходится, если 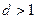, то есть если 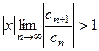, то есть .

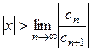Сравнивая с условием (6) получаем формулу (3).

Исследуем, ряд (5) с помощью признака Коши.

.

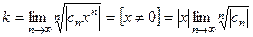Ряд (5) сходится, если 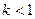, то есть если 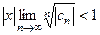, то есть .

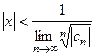Ряд (5) сходится, если 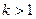, то есть если 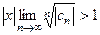, то есть .

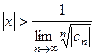Сравнивая с условием (6) получаем формулу (4).

■

I

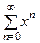. Здесь R=1,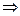 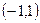- интервал абсолютной сходимост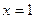и. При и при 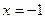ряд расходится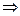 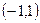- область сходимости ряда.

I

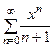. Здесь R=1,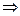 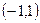- интервал абсолютной сходимости. При 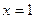ряд расходится, а при 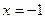ряд сходится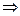 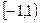- область сходимости ряда.

I

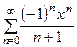. Здесь R=1,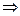 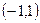- интервал абсолютной сходимости. При 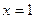ряд сходится, а при 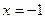ряд расходится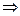 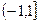- область сходимости ряда.

I

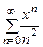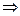
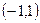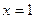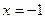. Здесь R=1, - интервал абсолютной сходимости. При и при ряд сходится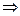 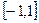- область сходимости ряда.