Сумма ряда (2) на интервале 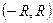 является непрерывной функцией.
является непрерывной функцией.
□
Пусть 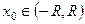 - произвольная точка. Пусть
- произвольная точка. Пусть 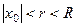 . На отрезке
. На отрезке 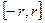 ряд (2) в силу Th 1 сходится равномерно
ряд (2) в силу Th 1 сходится равномерно 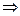 его сумма в силу теоремы о непрерывности суммы функционального ряда непрерывна на отрезке
его сумма в силу теоремы о непрерывности суммы функционального ряда непрерывна на отрезке 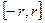 , а значит и в точке
, а значит и в точке 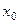 . А так как
. А так как 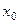 - произвольная точка интервала
- произвольная точка интервала 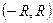 , то теорема доказана.
, то теорема доказана.
■
Из теорем о равномерной сходимости степенного ряда и теорем о почленном дифференцировании и интегрировании равномерно сходящихся функциональных рядов вытекают следующие теоремы.
Th 3. О почленном интегрировании степенного ряда.
Степенной ряд (2) можно почленно интегрировать от 0 до любого 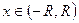 .
.
 2015-06-24
2015-06-24 839
839








