Th 6. О дифференцируемости суммы функционального ряда

Пусть все функции 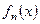функциональной последовательности непрерывно-дифференцируемы на отрезке 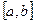(т.е. имеют непрерывную производную), причем функциональный ряд составленный из производных 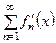равномерно сходится на этом отрезке. Тогда сумма функционального ряда (3) 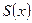дифференцируема на 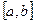, причем выполняется:

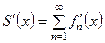. (19)

При этом говорят, что допустимо почленное дифференцирование функционального ряда.