(Жан Лерон Даламбер (1717 – 1783) – французский математик)
Если для ряда 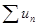 с положительными членами существует такое число q<1, что для всех достаточно больших n выполняется неравенство
с положительными членами существует такое число q<1, что для всех достаточно больших n выполняется неравенство 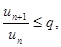
то ряд 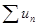 сходится, если же для всех достаточно больших n выполняется условие
сходится, если же для всех достаточно больших n выполняется условие 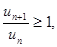 то ряд
то ряд 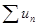 расходится.
расходится.
Теорема. (Предельный признак Даламбера является следствием из приведенного выше признака Даламбера.) Если существует предел 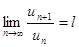 , то при
, то при 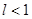 ряд сходится, а при
ряд сходится, а при 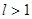 – расходится.
– расходится.
Если l = 1, то на вопрос о сходимости ответить нельзя.
Доказательство. Так как 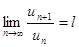 , то по определению предела для любого e>0 найдется натуральное число N такое, что при n>N выполняется неравенство
, то по определению предела для любого e>0 найдется натуральное число N такое, что при n>N выполняется неравенство 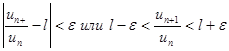 .
.
Пусть 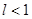 . Можно подобрать e так, что число l+e<1. Обозначим l+e=q, q<1. Тогда из правой части неравенства получаем
. Можно подобрать e так, что число l+e<1. Обозначим l+e=q, q<1. Тогда из правой части неравенства получаем 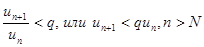 . В силу свойства числовых рядов можно считать, что
. В силу свойства числовых рядов можно считать, что 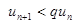 для всех n=1,2,3… Давая номеру n эти значения, получаем серию неравенств:
для всех n=1,2,3… Давая номеру n эти значения, получаем серию неравенств:
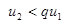 ,
, 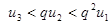 ,
, 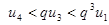 ,…,
,…, 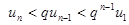 ,…
,…
т.е. члены ряда 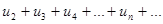 меньше соответствующих членов ряда
меньше соответствующих членов ряда 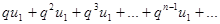 , который сходится как ряд геометрической прогрессии со знаменателем 0<q<1. Но тогда, на основании признака сравнения, сходится ряд
, который сходится как ряд геометрической прогрессии со знаменателем 0<q<1. Но тогда, на основании признака сравнения, сходится ряд 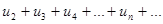 , следовательно, сходится и исходный ряд.
, следовательно, сходится и исходный ряд.
|
|
|
Пусть 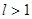 . В этом случае
. В этом случае 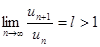 . Отсюда следует, что, начиная с некоторого номера N, выполняется неравенство
. Отсюда следует, что, начиная с некоторого номера N, выполняется неравенство 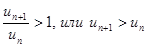 , т.е. члены ряда возрастают с увеличением номера n. Поэтому
, т.е. члены ряда возрастают с увеличением номера n. Поэтому 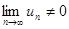 . На основании следствия из необходимого признака ряд
. На основании следствия из необходимого признака ряд 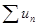 расходится. Ч.т.д.
расходится. Ч.т.д.
Пример. Определить сходимость ряда 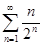 .
.
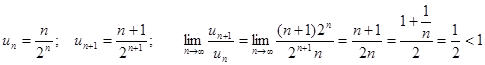 Вывод: ряд сходится.
Вывод: ряд сходится.
Пример. Определить сходимость ряда 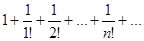
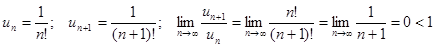 Вывод: ряд сходится.
Вывод: ряд сходится.
Пример. Определить сходимость ряда 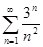 .
.
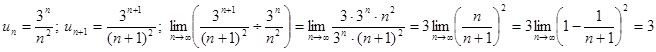
Вывод: ряд расходится.
 2015-06-24
2015-06-24 10355
10355








