Пусть даны два ряда 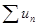 и
и 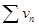 при un, vn ³ 0.
при un, vn ³ 0.
Теорема. Если un £ vn при любом n, то из сходимости ряда 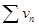 следует сходимость ряда
следует сходимость ряда 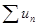 , а из расходимости ряда
, а из расходимости ряда 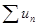 следует расходимость ряда
следует расходимость ряда 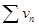 .
.
Доказательство. Обозначим через Sn и sn частные суммы рядов 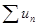 и
и 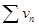 . Т.к. по условию теоремы ряд
. Т.к. по условию теоремы ряд 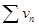 сходится, то его частные суммы ограничены, т.е. при всех n sn < M, где М – некоторое число. Но т.к. un £ vn, то Sn £ sn то частные суммы ряда
сходится, то его частные суммы ограничены, т.е. при всех n sn < M, где М – некоторое число. Но т.к. un £ vn, то Sn £ sn то частные суммы ряда 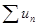 тоже ограничены, а этого достаточно для сходимости.
тоже ограничены, а этого достаточно для сходимости.
Пример. Исследовать на сходимость ряд 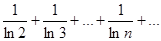
Т.к. 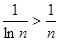 , а гармонический ряд
, а гармонический ряд 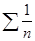 расходится, то расходится и ряд
расходится, то расходится и ряд 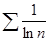 .
.
Пример. Исследовать на сходимость ряд 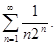
Т.к. 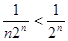 , а ряд
, а ряд 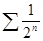 сходится (как убывающая геометрическая прогрессия), то ряд
сходится (как убывающая геометрическая прогрессия), то ряд 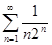 тоже сходится.
тоже сходится.
Также используется следующий признак сходимости:
Теорема (предельный признак сравнения). Если 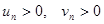 и существует предел
и существует предел 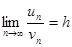 , где h – число, отличное от нуля, то ряды
, где h – число, отличное от нуля, то ряды 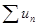 и
и 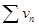 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Доказательство. По определению предела последовательности для всех n, кроме, возможно, конечного числа их, для любого e>0 выполняется неравенство 

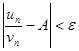 , или
, или 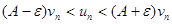 . Если ряд
. Если ряд 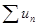 сходится, то из левого неравенства и теоремы(о сравнениии рядов) вытекает, что ряд
сходится, то из левого неравенства и теоремы(о сравнениии рядов) вытекает, что ряд 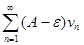 также сходится. Но тогда, согласно свойству числовых рядов, ряд
также сходится. Но тогда, согласно свойству числовых рядов, ряд 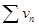 сходится.
сходится.
Если ряд 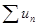 расходится, то из правого неравенства, теоремы и свойства вытекает, что и ряд
расходится, то из правого неравенства, теоремы и свойства вытекает, что и ряд 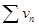 расходится. Аналогично в обратную сторону. Ч.т.д.
расходится. Аналогично в обратную сторону. Ч.т.д.
Пример. Исследовать на сходимость ряд 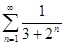 .
.
Сравним данный ряд с рядом геометрической прогрессии 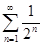 , который сходится (
, который сходится (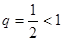 ). Имеем
). Имеем 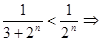 данный ряд сходится.
данный ряд сходится.
Пример. Исследовать на сходимость ряд 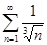 .
.
Возьмем ряд с общим членом 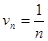 , который расходится (гармонический ряд). Имеем
, который расходится (гармонический ряд). Имеем 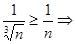 ряд расходится.
ряд расходится.
Пример. Исследовать на сходимость ряд 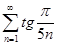 .
.
Применим предельный признак сравнения, возьмем 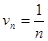 , который расходится. Так как
, который расходится. Так как 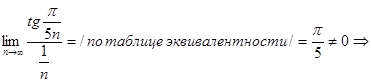 ряд расходится.
ряд расходится.
 2015-06-24
2015-06-24 2993
2993








