Пусть требуется вычислить 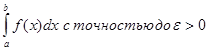 . Если подынтегральную функцию f(x) можно разложить в ряд по степеням х и интервал сходимости (-R;R) включит в себя отрезок [a;b], то для вычисления заданного интеграла можно воспользоваться свойством почленного интерирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функций.
. Если подынтегральную функцию f(x) можно разложить в ряд по степеням х и интервал сходимости (-R;R) включит в себя отрезок [a;b], то для вычисления заданного интеграла можно воспользоваться свойством почленного интерирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функций.
Пример. Вычислить интеграл 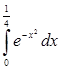 с точностью до
с точностью до 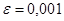 .
.
Расскладываем подынтегральную функцию в ряд Маклорена, заменив х на (-х2):
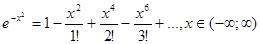 . Интегрируя обе части равенства на отрезке [0;1/4], лежащем внутри интервала сходимости, получаем:
. Интегрируя обе части равенства на отрезке [0;1/4], лежащем внутри интервала сходимости, получаем:
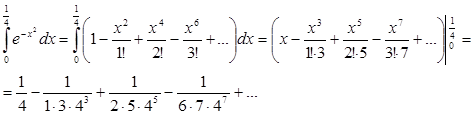
Получили ряд лейбницевского типа. Так как 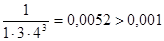 , а
, а 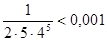 , то с точностью до 0,001 имеем:
, то с точностью до 0,001 имеем: 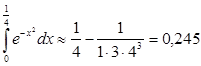 .
.
 2015-06-24
2015-06-24 754
754








