Ряд Фурье для функции f(x) периода Т = 2l, непрерывной или имеющей конечное число точек разрыва первого рода на отрезке [- l, l ] имеет вид:
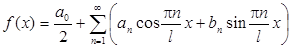
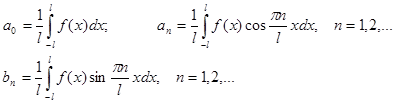
Для четной функции произвольного периода разложение в ряд Фурье имеет вид:
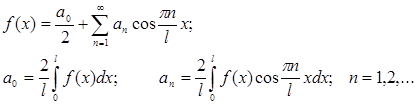
Для нечетной функции: 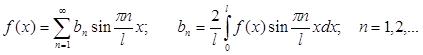
Пример. Разложить функцию f(x)=x на интервале (-4;4) в ряд Фурье.
Данная функция нечетная, удовлетворяет условиям Дирихле. По соответствующим формулам имеем, при 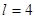 :
:
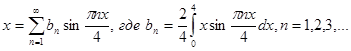
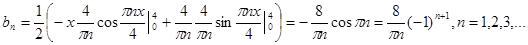
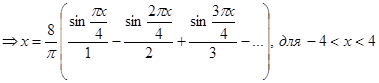 .
.
 2015-06-24
2015-06-24 1177
1177
