2015-06-26
513
Прежде всего, с помощью модели Уилсона находим оптимальный размер заказа для детерминированного случая
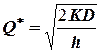
и период выполнения заказа
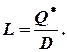
Затем, пользуясь вероятностным условием
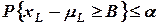, (1)
определяем размер резервного запаса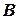 
.
Разделив неравенство
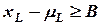
на величину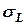 
, получим
.
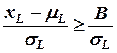Введем случайную величину
.
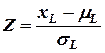Эта величина имеет нормальный закон распределения с параметрами:
,
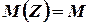
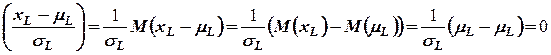
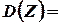
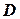
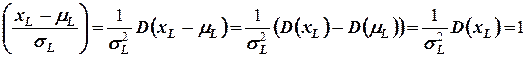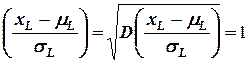
Таким образом, случайная величина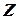 
является нормированной величиной с законом распределения 
.
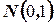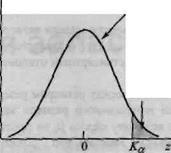
График дифференциальной функции распределения случайной величины 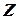изображен на рис.1
 |
 |
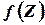
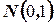
Рис. 1.
Из свойств нормального закона распределения следует, что вероятность того, что имеет место равенство
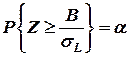
определяется по формуле
,
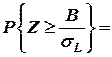
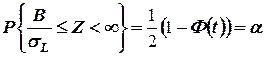Из последнего равенства находим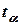 
.
Область, в которой выполняется неравенство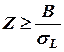 
на рис.1 обозначена 
.
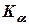Т.к.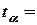 
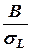, то 
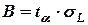
Следовательно, размер резервного запаса должен удовлетворять неравенству
.
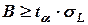Величина спроса на протяжении периода выполнения заказа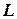 
обычно описывается плотностью распределения вероятностей, отнесенной к единице времени (например, к дню или неделе), из которой можно определить распределение спроса на протяжении периода .
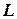В частности, если спрос за единицу времени является нормально распределенной величиной со средним значением 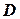и стандартным отклонением 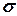, то общий спрос на протяжении периода выполнения заказа 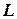будет иметь распределение 
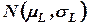, где 
= 
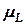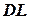и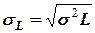 
.
На рис. 2 показана зависимость между размером резервного запаса 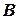ссредней величиной спроса 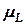на протяжении периода выполнения заказа и оптимальными значениями детерминированной модели экономического размера заказа 
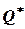и периода выполнения заказа 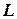.Заметим, что 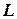должно быть равно эффективному времени выполнения заказа, как это определено в модели Уилсона.
Уровень Точки возобновления заказа
запаса
 |
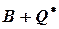
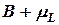
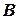
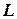
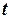
Рис. 1.
