Пример 4 – Построение линии пересечения конуса и цилиндра методом полных сечений

Метод вспомогательных сферических поверхностей (метод полных сечений) при построении линии пересечения любых тел вращения применяется в том случае если:

а) оси вращения этих тел пересекаются;

б) параллельны какой-либо плоскости проекции.

Применение метода секущих сфер основано на том, что пересечение шара с любым телом вращения, ось которого проходит через центр шара, проходит по окружности, которая проецируется в линию на одну из плоскостей проекций. Например, линии пересечения сферы с цилиндром и конусом – это окружности, 1' 2' и 3' 4' – фронтальные проекции этих окружностей 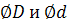. Далее определяем выполнение условий а) и б):

1. Оси вращения цилиндра и конуса проходят через центр сферы.

2. Оси вращения цилиндра и конуса параллельны фронтальной плоскости проекций.

Следовательно, линии пересечения цилиндра и конуса со сферой в этом случае окружности, которые на фронтальную плоскость проецируются в линии 1'2' и 3'4' (рисунок 5.9).

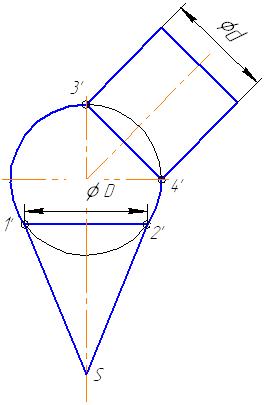
Рисунок 5.9 – Пересечение сферы с цилиндром и конусом

На рисунке 5.10 показано построение линии пересечения конической и цилиндрической поверхности с помощью вспомогательных концентрических сфер. Последовательность построения линии пересечения:

− определяем характерные точки, точки а ' и е' – точки пересечения очерковых образующих конуса и цилиндра;

− определяем вспомогательную сферу минимального радиуса.

Rd min – сфера минимального радиуса должна касаться одной из заданных поверхностей (конуса) и пересекать другую (цилиндр).

Сфера радиусом Rd min пересекает конус на окружности, фронтальная проекция которой является отрезок 1' 2', а цилиндр эта же сфера пересекает по окружности, фронтальная проекция которой является отрезок 3' 4'. На пересечений этих линий находится фронтальная проекция точки d',принадлежащая линии пересечения конуса и цилиндра;

− определяем вспомогательную сферу максимального радиуса. Ra max – радиус сферы равен расстоянию от центра до наиболее удаленной точки линии пересечения. С помощью этой сферы получаем точку а^',принадлежащей линии пересечения конуса и цилиндра.

− для нахождения промежуточных точек фронтальной проекции линии пересечения b ' и c ' применяют сферы, радиусы которых лежат в пределах Rd min d wsp:val="00FF6AA1"/><wsp:rsid wsp:val="00FF7AD6"/></wsp:rsids></w:docPr><w:body><w:p wsp:rsidR="00000000" wsp:rsidRDefault="00BD7276"><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/></w:rPr><m:t>&lt;R &lt;Ra max</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> ;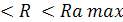

− по найденным точкам а ', b ', c ', d ', e ' проводим фронтальную проекцию линии пересечения.

Горизонтальную проекцию линии пересечения строим по правилам начертательной геометрии, а именно, принадлежности точки поверхности. Через точки b ', c ', d ' проводим образующие конуса и по линии связи на горизонтальной плоскости проекции находим точки b, c, d, принадлежащей линии пересечения конуса и цилиндра. Точки а' и е' находятся на очерковой образующей конуса – S - VII.

Для построения разверток конуса и цилиндра делим основания поверхностей на 12 равных частей и строим развертки по общим правилам (рисунки 5.11 и 5.12).

Смотри примеры 5.1, 5.2, 5.3.

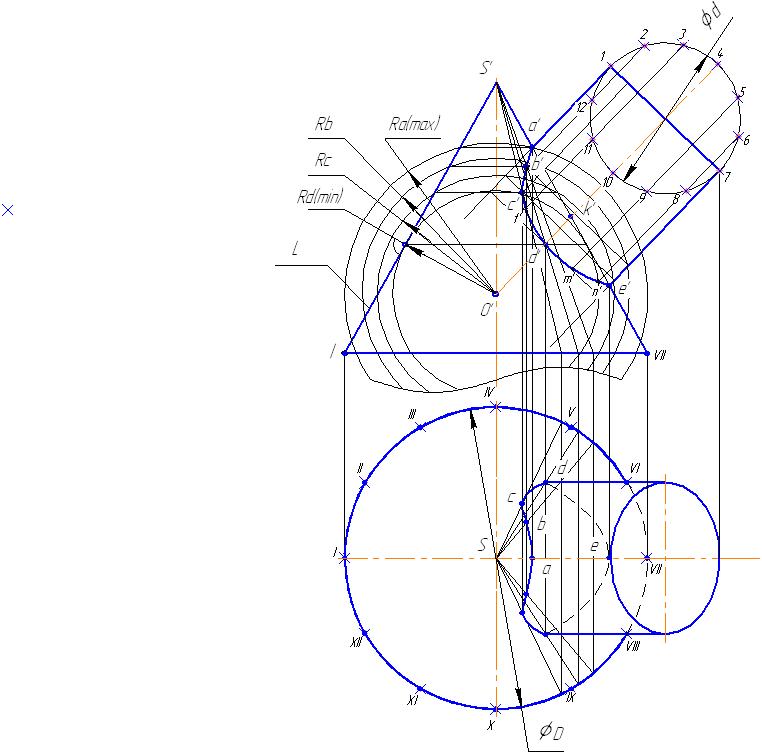
Рисунок 5.10 – Пересечение конической и цилиндрической поверхностей

Рисунок 5.11 – Развертка цилиндра

Рисунок 5.12 – Развертка конуса