В.Н. Новоселицкого, Л.А. Гершанок

Ранее указывалось, что над залежами нефти и газа установлены зоны изменения химического состава и намагниченности пород. Причиной таких изменений является литолого-фациальная неоднородность осадочного покрова в горизонтальном направлении. Задача определения характера латеральной изменчивости намагниченности осадочных отложений при поисках залежей нефти и газа является первоочередной. Этот вопрос в литературе исследован недостаточно. Рассмотрим один прием определения намагниченности осадочных пород по магнитным аномалиям при аппроксимации разреза горизонтально-слоистой моделью с вертикальной намагниченностью, переменной в литеральном плане /3/.

Исходные уравнения можно получить из выражения для магнитного потенциала

U= 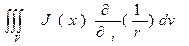, (11.14)

где i ‑ направление намагниченности J(х). Введем обозначения глубин для горизонтального бесконечного пласта: h₁ – глубина кровли пласта и h₂ – глубина подошвы пласта. После преобразований при фиксированном начале координат для случая двухмерного распределения переменной вертикальной намагниченности получим

Z(x) = 2 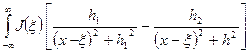d 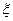. (11.15)

Относительно функции J(x) это равенство является интегральным уравнением первого рода типа свертки.

Если функции J(x) и Z(x) удовлетворяют условиям

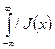d х / < + ∞, 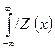d х / < + ∞,

то выражение в квадратной скобке уравнения (11.15) обозначим как K(x). Применим преобразование Фурье

S_z(ω,о) = 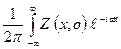dх, (11.16)

S_J (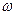) = 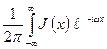dx, (11.17)

S_k (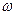) = 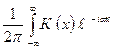dx = 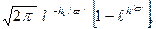, (11.18)

h = h₂ – h₁.

Пользуясь теоремой о свертке функций, определим Фурье-образ функции вертикальной составляющей напряженности

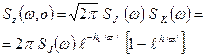. (11.19)

Отсюда Фурье-образ функции намагниченности примет вид

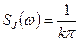
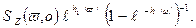(11.20)

Так как ось z направлена вниз, то

S _z (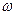) 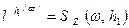, (11.21)

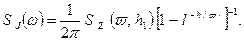(11.22)

Выражение в квадратной скобке представим рядом по степеням

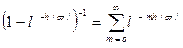. (11.23)

Для Фурье-образа намагниченности получим

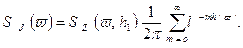(11.24)

В пространстве оригиналов имеем

J (x) = 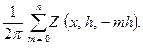(11.25)

Здесь первое слагаемое ряда, полученного при m= 0, есть значение вертикальной составляющей, аналитически продолженное вниз на верхнюю кромку намагниченного тела; последующие члены ряда ‑ значения Z, перечисленные вверх с шагом, равным мощности пласта.

Если бы наблюдения были проведены непосредственно на поверхности пласта, то вычисление значения намагниченности сводилось бы к суммированию по известным схемам аналитически продолженных вверх значений:

J (x) = 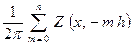. (11.26)

Физический смысл становится понятным и в предельном случае, когда имеется горизонтальный пласт большой мощности (2b>h), заполняющий все нижнее полупространство. Тогда влияние нижней поверхности равно нулю, а намагниченность определяется по формуле

J (x) = 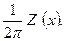(11.27)

Эта формула довольно часто применяется на практике для определения латеральной намагниченности горных пород.