Основы структурно-параметрической оптимизации

Пусть система автоматического управления представлена следующей структурной схемой (рис. 3).

Передаточная функция по каналу задания имеет вид:

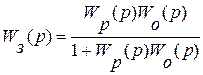(20)

Передаточная функция по каналу возмущения имеет вид:

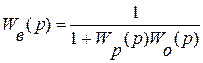(21)

При синтезе алгоритмической структуры системы управления должны выполняться следующие требования:

· система должна как можно лучше, точнее воспроизводить любые изменения задающего воздействия 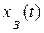на выходе объекта управления :

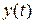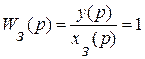(22)

· система должна как максимально лучше устранять влияние возмущений на управляемую величину :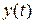

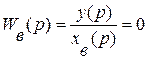(23)

· система должна быть устойчивой.

Однако на практике условия (22), (23) невозможно реализовать технически, поэтому задаются более реальными условиями:

· по каналу заданий:

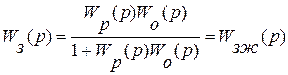(24)

где 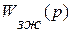- желаемая передаточная функция системы управления по каналу задания, обладающая желательными статическими и динамическими свойствами.

· по каналу возмущений:

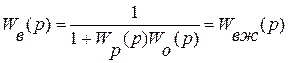, (25)

где 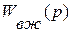- желаемая передаточная функция системы управления по каналу возмущений, обладающая желательными статическими и динамическими свойствами.

Пусть объект управления задан передаточной функцией следующего вида:

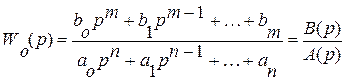(26)

Желаемая система управления представлена передаточной функцией следующего вида:

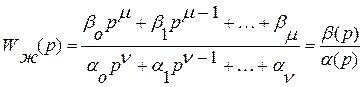(27)

Тогда передаточная функция регулятора в соответствии с (25) и (24) будет иметь следующий общий вид:

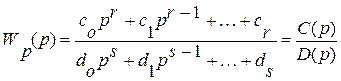(28)

Передаточная функция регулятора в системе управления по заданию будет иметь вид:

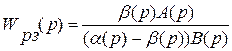(29)

Передаточная функция регулятора в системе управления по возмущению будет иметь вид:

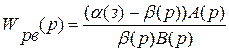(29)

Для физической реализуемости в передаточной функции замкнутой системы порядок числителя 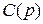должен быть не больше порядка знаменателя 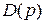. Для систем управления по заданию:

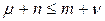(30)

Для систем управления по возмущению:

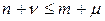(31)

Условия (30) и (31) можно переписать в следующем виде:

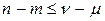(32)

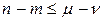(33)

При решении практических задач синтеза выбор желаемых передаточных функций ограничивается определенными формами, которые называются стандартными и которые имеют более простой вид:

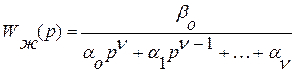(34)

Коэффициент числителя 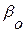, исходя из условия статики 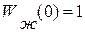, принимают:

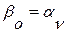(35)

А коэффициенты знаменателя 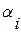выбирают по одной из стандартных форм.

Простейшая стандартная форма называется биномиальной и ей соответствует желаемая передаточная функция вида:

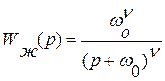(36)

Характеристические полиномы, соответствующие биномиальной форме представлены в таблице

Порядок системы	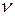Характеристический полином

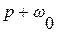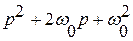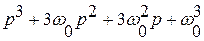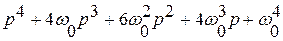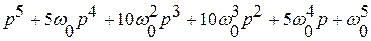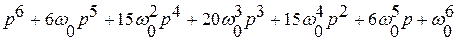Простейшая биномиальная форма желаемой передаточной функции соответствует последовательному соединению из 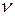апериодических звеньев с постоянной времени 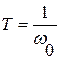. Данная система имеет один корень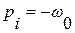 . Согласно корневым методам оценки качества такой системе будет соответствовать апериодический переходный процесс с временем переходного процесса 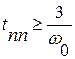. Поэтому параметр 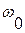называют степенью быстродействия

Таким образом, настройка системы на биномиальную передаточную функцию обеспечивает следующие показатели качества 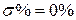и .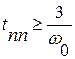

Более часто используется стандартная форма Баттерворта (фильтр Баттерворта). Характеристический полином фильтра Баттерворта имеет 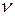отрицательных корней, которые расположены на дуге с радиусом 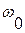, отстоящих друг от друга 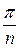и определяются по формуле:

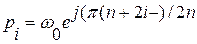(37)

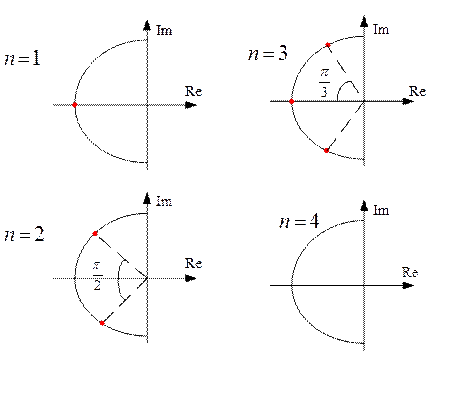
Характеристические полиномы, соответствующие форме Баттерворта представлены в таблице

Порядок системы	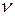Характеристический полином

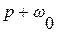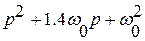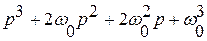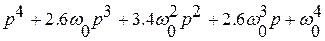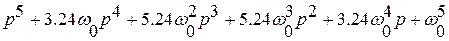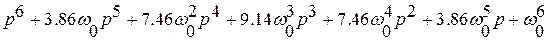Рассмотрим более подробно фильтр Баттерворта