Оптимальный объем выборки

В биологических исследованиях часто заранее требуется установить число наблюдений, достаточное для получения репрезентативных оценок генеральной совокупности.

Для непрерывных признаков метод состоит в том, чтобы, используя известные соотношения между средней, стандартным отклонением, ошибкой средней, плотностью вероятности распределения Стьюдента, найти число степеней свободы, соответствующее доверительному интервалу для средней при уровне значимости α = 0.05. Объем выборки, достаточной для получения результата за­данной точности, находят по формуле:

,

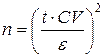где п – объем выборки,

t – граничное значение из таблицы распределения Стьюдента (табл. 6 П), соответствующее принятому уровню значимости при планируемом объеме выборки,

CV – приблизительное значение коэффициента вариации (%),

ε – плани­руемая точность оценки (погрешности) (%).

Рассчитаем необходимый объем условной выборки, обеспечивающий хорошую точность ε = 3%, для уровня значимости α = 0.05 (t = 1.98, для df ≈ 100) и для коэффициента вариации CV = 12% (такова относительная изменчивость многих размерно-весовых признаков животных):

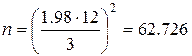≈ 63 экз.

Если исследуется фенотипическое (видовое) разнообразие (дискретный признак), может возникнуть задача определения минимального объема выборки, в которой будет присутствовать хотя бы один экземпляр с определенным фенотипом (Животовский, 1991). С позиций теории вероятности задача ставится так: определить объем выборки, в которой с вероятностью P можно ожидать присутствие особи с признаком, частота которого в генеральной совокупности составляет π. Предлагается следующая формула:

.

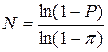В первом приближении значение π можно определить приблизительно по имеющимся данным. Что же касается вероятности P, то ее уровень довольно сильно влияет на величину необходимого объема выборки. Для большей надежности следует брать P = 0.99, но тогда возрастет объем работ; не столь высокие требования (P = 0.95) могут и не позволить найти искомый фенотип. В частности, при уровне вероятности P = 0.95 и предположительной частоте фенотипа в популяции π = 0.05 потребуется

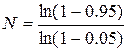= 58.4 ≈ 59 экз.,

чтобы отловить хотя бы одну особь с этим дискретным признаком.

оценка принадлежности варианты к выборке

Иногда встречается ситуация, когда одна из полученных вариант сильно отличается от остальных. Можно ли такие резко выде­ляющиеся значения использовать при дальнейших расчетах? В терминах математической статистики поставленный вопрос звучит так: относится ли данная варианта вместе с другими вариантами изучаемой выборки к одной и той же генеральной совокупности или – к разным? Его можно сформулировать и по-другому: сформировано ли данное значение варианты под действием тех же доминирующих и случайных факторов, что и все остальные варианты данной выборки, или это были иные факторы? Здесь возможны два ответа.

1. Факторы те же, т. е. все варианты взяты из одной и той же генеральной совокупности.

2. Факторы иные, т. е. особенная варианта и выборка порознь взяты из разных генеральных совокупностей.

Ответ на этот вопрос можно получить с использованием рассмотренных выше свойств нормального распределения. Так, если все варианты были взяты из одной генеральной совокупности, значит, они должны отличаться друг от друга только в силу случайных причин и (с вероятностью P = 0.95) находиться в диапазоне M ± 2 ∙ S. Иными словами, по случайным причинам варианты достаточно большой выборки будут отклоняться влево или вправо от средней арифметической не более чем на 2 ∙ S: x − M < 2 ∙ S или (x − M)/ S < 2.

Эта величина, нормированное отклонение, и служит безразмерной характеристикой отклонения отдельной варианты от средней арифметической:

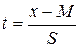~ t_{табл .},

где t – критерий выпада (исключения),

x – выделяющееся значение призна­ка,

М – средняя величина для группы вариант,

t_табл. – стандартные значения критерия выпадов, определяемые свойствами нормального распределения, их можно найти по табл. 5 П для трех уровней вероятности (для больших выборок обычно пользуются значением t_табл. = 2 при P = 0.95, или α = 0.05).

Для вариант, принадлежащих изучаемой достаточно большой выборке, нормированное отклонение меньше двух (с вероятностью P = 0.95): t < 2. В случае действия на варианту некоего необычного фактора, она окажется за пределами указанного диапазона M ± 2S, и ее нормированное отклонение будет равно или больше двух: t ³ 2.

Нормированное отклонение есть простейший статистический критерий, который помогает определять так называемые «выскакивающие» варианты и решать вопрос о возможности их отбрасывания как артефактов (исключать из дальнейшей обработки). После такой «чистки» параметры выборки должны быть рассчитаны заново. К оценке чужеродности вариант, как и к другим методам статистики, нельзя подходить формально; цель биометрического исследования всегда состоит в том, чтобы понять специфику явления. В частности, «отскакивающая» варианта может быть следствием того, что признак имеет иное, не -нормальное распределение.

Рассмотрим работу критерия на примере. При измерении длины черепа взрослых самцов обыкно­венной землеройки-бурозубки получены выборки с такими па­раметрами: М = 18.8, S = 0.3 мм. Общее число животных n = 85. Среди прочих вариант два больших значения (19.2 и 21.0) вызывали сомнения. Определим для них критерии выпада:

, .

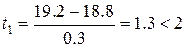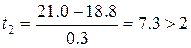Согласно таблице 5 П, критическое значение нормированного отклонения для уровня значимости α = 0.05 и n = 85 равно t = 2.0. Поскольку первое полученное значение (1.3) меньше табличного (2), первый из сомнительных результатов исключать не следует, а второй должен быть отброшен – критерий выпада (7.3) превышает таб­личное значение (2).

Понятие нормированного отклонения позволяет ввести важнейшее понятие статистики. Статистика – безразмерная случайная величина, которая имеет известный закон распределения и используется в качестве критерия для проверки статистических гипотез.

В этом смысле нормированное отклонение есть статистика. Во-первых, это безразмерная величина, поскольку единицы измерения числителя (x_i − M) и знаменателя (S) взаимно уничтожаются. Во-вторых, нормированное отклонение имеет вполне определенное распределение (в случае непрерывных признаков – нормальное) со своими параметрами (рис. 9). Его средняя равна нулю M_t = t_M = (M − M) / S = 0, а стандартное отклонение равно единице S_t = t_S = (S − M) / S = (S − 0) / S = S / S = 1.

Рис. 9. Переход от реального признака x к нормированному отклонению t

Нормированное отклонение – универсальная величина. Какой бы признак (имеющий нормальное распределение) мы ни брали, его значения можно выразить в виде расстояния от центра в единицах стандартного отклонения, т. е. на сколько S данное значение x отклонилось от M. При этом, как следует из свойств нормального распределения, крайние значения в 95% случаев не будут принимать значения меньше −2 и больше 2.

С помощью нормированного отклонения можно, например, оценивать отличия разнокачественных объектов (пород и сортов, ви­дов, популяций, генераций и пр.), причем даже по разным признакам.

Нормированное отклонение можно использовать и для срав­нительной оценки разных индивидов по одному и тому же признаку. Например, если сопоставляемые по относительному весу сердца молодая и взрослая землеройки-бурозубки демонстрируют оди­наковые показатели (10.5 мг%), то это, тем не менее, не озна­чает их сходства по изучаемому признаку. Используя известную информацию (у молодых средний индекс сердца равен M = 10.0 при стандартном отклонении S = 1.3, у взрослых – M = 11.8, S = 1.1), рассчитаем нормированное отклонение для молодого зверь­ка 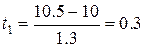и для взрослого 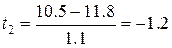. Налицо существенное различие: взрослый зверек имеет относительно низкий показатель сердеч­ного индекса, а молодой близок по этому признаку к ви­довой норме.

Наибольшее развитие такой подход получает в процедурах обработки многомерных данных, при исследовании объектов, охарактеризованных по многим признакам, методом корреляций, главных компонент, при их кластеризации и т. п. Во многих случаях обработка многомерного массива начинается с нормирования данных по формуле нормированного отклонения.